d1 (+ ½ )<--*---[ o ]----*-->(- ½ ) d2
Orthodox
quantum mechanics forbade the simultaneous measurement of a property (say
different spin states) for the same system. If you got one, you could not
obtain the other. This was a direct outcome of the Heisenberg Indeterminacy
Principle which stated that simultaneous quantum measurements could not be made
to the same precision.
E-P-R argued that this showed the incompleteness of quantum mechanics. It was not the 'paragon' of physical theories its apologists claimed, especially if such indeterminacy was fundamentally embedded within it.
But years later, in 1964 (as I noted) mathematician John S. Bell asked the question: 'What if the E-P-R experiment could actually be carried out? What sort of mathematical results would be achieved?'
In a work referred to as "the most profound discovery in the history of science", Bell then proceeded to place the E-P-R experiment in a rigorous and quantifiable context, which could be checked by actual measurements.
Bell made the basic assumption of locality (i.e. that no communication could occur between the detector d1 and detector d2 at any rate faster than light speed). In what is now widely recognized as a seminal work of mathematical physics, he set out to show that a theory which upheld locality could reproduce the predictions of quantum mechanics. His result predicted that the above sum, S, had to be less than or equal to 2 (S less than or equal 2). This became known as the 'Bell Inequality'.
The original form of the experiment invoked the quantum state of a two particle system in which position differential (x1 - x2) and momentum sum (p1 + p2)are both determined. Then the wave function is:y (x1, x2) = f(x1 - x2 -a) = å ¥ k=0 c k exp[ik(x1 - x2 -a)]
where the summation is over the k elements; f(x1 - x2 -a) is a packlet function sharply peaked at (x1 - x2) = a. Alternatively, if p is measured, then one knows immediately that p2 = -p1 since p1 + p2 = 0. In both cases the 1st particle is "disturbed" by measurement and this accounts for the Heisenberg uncertainty relations applied in 1-d. However, the 2nd particle is taken not to interact with the 1st at all- so one can obtain its properties minus the assumption of any disturbance.
The
first highly refined experiments to test quantum conformity to Bell's Theorem
were performed by Alain Aspect and his colleagues at the University of Paris.[2] In
these experiments, the detection of the polarizations of photons was the
key. These were observed with the photons emanating from a Krypton-Dye laser
and arriving at two different analyzers A1 and A2, e.g.
But even they were forced to admit (p. 312):
"One can escape the foregoing argument, deriving nonlocality from quantum mechanics, only by giving up the experimenter's free choice, i.e. by assuming superdeterminism."
By that they meant the two detectors at A1, A2 would only be able to obtain measurements as prescribed by quantum mechanics provided the decisions for determination (say of the polarizations of the photons) were "pre-coordinated". One would then obtain "nonlocal pre-coordination" between mutually distant measurement events. The authors concede this is "far more beyond current conceptions than a simple nonlocal influence", but also argued it could not be "absolutely excluded".
Well, ok, but in the same vein the sudden migration of all the air molecules in the room I'm in - say to one corner- suffocating me, cannot also be "absolutely excluded" from happening. But I am not terribly worried that it will.
The mighty success of the Aspect/Clauser experiments as well as Zeilinger's quantum teleportation proposal has been more than amply demonstrated with the kind of secure communications used in China's Micius satellite (see link to a previous post I wrote, below).
In ending it is important to bear in mind just how violently opposed Einstein was to the whole notion of quantum mechanics, especially the uncertainty or indeterminacy principle. This is what elicited his famous "God does not play dice with the universe" quote and which initiated a debate with Neils Bohr that went on for some time, even before the E-P-R experiment. To get an idea of the lengths Einstein went to, in order to prove Bohr (and quantum mechanics) wrong, it is instructive to check out this earlier post below- which includes the ingenious device Einstein conceived to try to trip up Bohr. It is well worth a read again, especially that section to do with Einstein's thought experiment:
See Also;

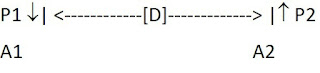

No comments:
Post a Comment