The Denver Post article 'Rockets Teach Students Physics' was a joy to read, describing as it did how model and amateur rocketry now being used as part of AP Physics in select Colorado high schools. It also brought back memories of my own rocket launches at Monsignor Pace High School (in Miami) in 1962-63, when the entire school would be released to witness a launch. One of my own single stage rocket designs, including dimensions of the fins, tubing etc., is shown below:
In the case of the Colorado exploits, one learned from the Post that :
"Nearly 100 students from Severance and Windsor high schools robotics and AP physics classes took their work into the field, launching their rockets from a practice field on the north side of Windsor high and middle schools."
Behind the eventual success of those launches - working as a technical adviser - was Matt Rhode, a University of Colorado aerospace engineering sciences instructor. He patiently saw the physics students through critical steps in the problem - solving of why several 'birds' failed to ignite on their respective pads.
One of the problems encountered was a repeated failure, even on the first or second attempt. Rhodes then showed the problem could be traced to two wires in contact in the ignition system, shorting it out. As one Severance HS student summed up the issue:
“Technology is a bit confusing still. Just a problem so simple, just two wires touching wouldn’t make it work.”
Well, that's rocketry , my young friend! But you won't find a more worthwhile vehicle (no pun intended) to get into the Newtonian content of AP physics. Just the launch of a single rocket can teach an abundance of principles, as well as their application. Consider just the thrust needed to propel a rocket of a given weight W:
Let's say the model rocketeer wishes to compute the velocity v2 from the equation above, using the units (feet-pounds) as indicated. Let the total impulse of the engine be 10 pound-seconds, and the burn time of the engine be 2 seconds. Then the force F or thrust is:
(10
lb-sec)/ 2 sec x (16 oz/ 1 lb) = 80 oz.
Then
the velocity v2 = (80 oz/ 10 oz - 1) 32 ft/ sec/sec (2 sec)
Assuming
the average weight of the rocket at lift off is 10 oz.
v2 = (8
- 1) (64 ft/ sec) = 7( 64 ft/ sec)= 448 ft/ sec or about 135
m/sec
Which
is a reasonable value.
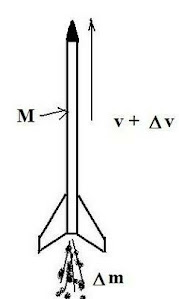
Then one can go into detail using integral calculus as well, incorporating changes in momentum. We can use the diagram below as a working template:
The rocket’s motion changes when a fraction of its mass (D m) is released in the form of ejected gases. Since the gases acquired their own momentum, the rocket receives a compensating momentum in the opposite direction. Therefore, the rocket is accelerated as a result of a push from the gases. In free space, or a vacuum, the entire system works independent of the presence of any opposing medium. Assume at some time t, the momentum of the rocket plus fuel is:
(M + D m)v,
then at some later time: (t + D t), the rocket ejects some fraction of mass D m, so the rocket’s velocity must increase to (v + D v). By appealing to Newton’s 3rd law via an application of conservation of momentum, we may write:
Total initial momentum of the rocket system = Total final momentum of the system
Then we get:
(M + D m)v = M(v + D v) + D m(v – v’)
Where v’ is the velocity with which the fuel is ejected relative to the rocket. The equation can then be simplified to yield: Mdv = v dm, which may be integrated, viz.:
M ò v1v2 dv = v òm1m2 dm
Or,
letting m2 = M f, m1 = M i and
v2 = v f, v1 = vi:
v f – vi: =
v’ ln [M i / M f]
Where the left side shows the difference between the final
and initial velocities, M i refers to the initial
rocket mass (fuel plus rocket proper) and M f refers
to the final rocket mass with fuel expended. (In general, for
most rockets, M i >>
M f ).
We have: M i = 1.0 kg, M f =
0.05 kg
Therefore, the difference between initial and final
velocities is:
v f – vi: = v’
ln [M i / M f]
v f – vi: =
(100 m/s) ln [1.0 kg/ 0.05kg]
v f – vi: = (100 m/s) ln(20) = (100 m/s) (3) = 300 m/s
The altitude can be estimated by using the kinematic eqn.
s = ½ at2
where s is the vertical displacement for an acceleration a, over time t.
s = ½ (300 ms-2) (3)2
s = 450 m or 1 485 ft.
In Barbados, teaching A-level physics at Harrison College, a number of students expressed interest in 'hard core' amateur rocketry - not just the model rocketry using carboard tubes and pre- built motors. While we lacked the open field facilities to conduct launches, given the College location in the city of Bridgetown, we at least explored the principles needed for design, especially of a proper rocket nozzle - which students were then encouraged to make in the lab. Of inestimable use was Capt. Bertrand Brinley's fine text:
The computation for the effective thrust coefficient CF shown at the bottom is related to the physical specs including the atmospheric pressure, Pa , the chamber pressure, Pe , the ratio of specific heats (Cp /Cv ) for combustion products k . The combustion chamber cross-sectional area (Ae / A t) is the ratio of nozzle exhaust area to throat area) given by:
(Ae /
A t) =
(M t / M c) [(1
+ M c 2 (k -1 )/2/ 1
+ M t 2 (k
-1 )/2] k+1/2(k+1)
Where M t is
the Mach number of the gases in the throat, and M c is
the Mach number at the end of the cylindrical section.
Generally, the diameter of the nozzle throat needs to be about one third the
diameter of the combustion chamber, while the angle of the converging section
of the nozzle needs to be approximately 30 degrees, and the angle for the
diverging section 15 degrees. The failure to properly design the nozzle is
probably responsible for most amateur rocket misfires.
But as two Colorado students: one
"Trial and error is definitely the biggest part. If something doesn’t work, with engineering, you have to figure out why it doesn’t work. It didn’t work the first couple of times, but you try, try, try again.”
"This rocketry is something real, as opposed to problems on a worksheet or in a textbook" as one of the physics advisors said. Which is exactly why rocketry - whether model or amateur- remains a great way to teach Newtonian physics, at AP, or A-level. Similarly, it can be argued that using physics applications to teach algebra - is a great way to teach that subject:
See Also:
https://ocw.mit.edu/courses/aeronautics-and-astronautics/16-346-astrodynamics-fall-2008/
And:
And:





No comments:
Post a Comment