Feynman teaching quantum mechanics at Caltech, 1962
Physicist Ian Durham - writing in the January Physics Today ('Teaching Quantum Concepts') is absolutely correct that:
"quantum computing seems to grab the headlines, quantum mechanics lies at the heart of a vast array of fields, including modern electronics and modern medicine—not to mention all of chemistry."
And yet, "it is also a notoriously obtuse subject in many ways."
One of the main problems is:
"there’s no clear consensus on what represents the bare-minimum competency in quantum mechanics, and there is even less consensus on the best formalism to use."
The last is likely because there are different formalisms, for example Erwin Schrodinger's differential equations vs. Pauli's matrices and then Dirac's own with 'bras' and 'kets'. Beyond that, and as physicist Richard Feynman once put it in his 'Lectures on Physics', it’s easy to fall down a rabbit hole when attempting to convey quantum ideas to an audience for the first time. In his Lectures on Physics (Vol. II, Preface, p. 4) he remarked on his own shortcomings teaching QM as part of a Caltech physics course:
"The usual way of dealing with quantum mechanics makes that subject almost unavailable for the great majority of students because they have to wait so long to learn it. Yet in its real applications, such as chemistry and electrical engineering, the full machinery of the differential equation approach is not actually used. So I tried to describe the principles of quantum mechanics in a way in a way which wouldn't require one first know the mathematics of partial differential equations. Even for a physicist I think that is an interesting thing for a physicist to try to do - to present quantum mechanics in this reverse fashion...However, I think that this experiment in the quantum mechanics part was not completely successful - in large part because I did not really have enough time at the end."
But in truth, even given enough time (Feynman goes on to cite "energy bands and the spatial dependence of amplitudes") it is doubtful he would have been successful in his teaching of QM. A point even conceded by Matthew Sands (one of the co-authors of the 'Lectures' in his Physics Today piece on them (April 2005, p, 49) noting:
"Some students had difficulty separating the key ideas in the lectures from some of the secondary material introduced to provide illustrative applications. This was particularly frustrating when studying for examinations."
And as Sands noted (ibid.) "fewer than half were planning to be physics majors." Which would have contributed mightily to student confusion, given non-specialists are more likely to treat equally topics presented, irrespective of import. Durham himself goes on to note:
"Analogies only go so far in the quantum world, since it is so far removed from our everyday experience. For example, I have found that some people have difficulty even grasping the notion of discrete energy levels, let alone understanding the notoriously murky subject of entanglement. And yet both of those ideas are important enough that they should be understood by more people."
Feynman also pointed such difficulties in his 'Lectures', (ibid.)
"We know how large objects will act but things on a small scale simply do not act that way. So we have to learn about them in a sort of abstract of imaginative fashion, and not by connection with our direct experience." Adding some pages later: "I don't think I did very well by the students. When I look at the way the majority of the students handled the problems on the examinations, I think that the system is a failure."
What did he mean? He actually answered it a paragraph earlier when he admitted: "I now believe quantum mechanics should be given at a later time." In other words, as he first intimated, at a time the student either has taken differential equations already (as a prerequisite) or is taking such course concurrently. The reason being that the 'mysteries' of QM only come to light by resorting to the analysis available from such equations.
I still recall teaching a Calculus physics course for which the final chapter of the text assigned had significant quantum mechanics content, including: the basic Schrodinger wave equation, quantum square well, atomic energy levels, eigenvalues, probability densities and how to compute expectation values. Attached below is one problem which I worked out for the class:
But which only 1-2% of the class actually got. Most were stung by: a) not having the requisite mathematical ability (which makes one wonder how they managed to be allowed to move on from the earlier semesters) and b) not being able to conceptualize, despite numerous visual aids. One of the visual aids which flummoxed them is shown below:
The diagram remained mostly meaningless. As with Feynman's Caltech class, most of my students did not plan to be physics majors. They had merely signed on to Calculus Physics because it was listed as a pre-requisite for entry into a pre-med program. I believe this is what Feynman meant when he opined "the system is a failure". Why? Because there is no way in hell any pre-med student would actually take a class in partial differential equations - or even differential equations - to grasp quantum mechanics.
Ian Durham also alludes to these difficulties in his essay and the fact that linear algebra is a much easier 'fish' to fry, e.g.:
"In a computer science
setting, it’s much easier to introduce basic quantum concepts by using linear
algebra than, say, a strict calculus-based formalism that emphasizes
differential equations. In fact, I tend to find that the algebraic approach is
easier even with physics majors."
So what to do? Prof. Durham's solution may be the one to consider, as he writes (ibid.):
"Unfortunately, there is no simple, one-size-fits-all method. It would certainly help matters if people were introduced to quantum concepts at multiple points through a variety of techniques during their K–12 education, but that would require changing standards and increasing the number of teachers who have been exposed to those ideas."
But can the system be repaired sufficiently to allow this changing of standards? That remains to be seen. Feynman's own takeaway from his Caltech physics teaching experience was sobering and bears attention from any physics educator, lecturer (op. cit., Lectures, Pt. II, p 6);
"The best teaching can be done only when there is a direct individual relationship between a student and a good teacher—a situation in which the student discusses the ideas, thinks about the things, and talks about the things. It's impossible to learn very much by simply sitting in a lecture, or even simply by doing problems that are assigned."
Adding with as a dose of reality:
"But in modern times we have so many students to teach (in large lecture hall classes) that we have to try to find some substitute for the ideal."
It may well be that Prof. Durham's solution is the optimal one.
To see Yale Professor Ramamurti Shankar's QM lecture on the same 'particle in a box' go to:
PHYS 201 - Lecture 23 - Quantum Mechanics V: Particle in a Box | Open Yale Courses
To compare with an MIT (open courseware) lecture, go to:
Infinite square well energy eigenstates (13:15)
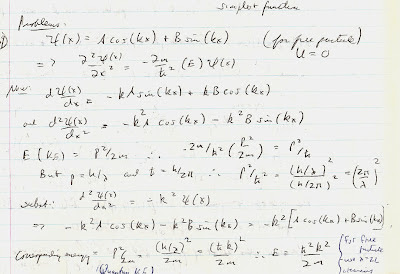
No comments:
Post a Comment