Revisiting Basic Nuclear Physics (4) - Nuclear Fusion

 Nuclear Fusion Reactions:

 In general a nuclear fusion reaction is one in which two light nuclei combine (fuse) to form a heavier nucleus with positive energy given off (the Q of the reaction).  Nuclear fusion is demonstrated in its most compelling form in the case of stellar energy. Exhaustive investigations in this regard, eventually led to the realization that fusion was the only practical energy by which stars could be sustained over long periods of time, such as billions of years.

In the Sun, for example, two distinct nuclear fusion processes occur: 1) the proton-proton cycle, and 2) the carbon-nitrogen cycle.   In the first of these (the easier one because it has fewer reactions):                                                                                     

¹H + ¹H + e^- ®  ² H   + n + 1.44 MeV

² D   + ¹H ®  ³ He + g + 5.49 MeV

³ He + ³ He ®  ⁴ He + ¹H + ¹H  + 12.85 MeV

The top line shows two protons fusing to yield deuterium (heavy hydrogen) with a positron and neutrino (n) emitted, along with 1.44 MeV of energy. Empirical evidence of this reaction is obtained from gallium detectors, of the neutrinos given off, which are within 1-2% of what theoretical models predict.[1] In the second fusion reaction, the deuterium combines with a proton to give the isotope helium 3, along with a gamma ray (g) and 5.49 MeV energy. In the final fusion, two helium-3 nuclei combine to yield one helium-4 nucleus, along with two protons, and 12. 85 MeV energy. Note that the two ending product protons commence the cycle anew, so that the generation of nuclear energy is ongoing.  

The ending quantities on the right sides of each part of the cycle denote the Q of the reaction for that part.  Let us check the Q for the first and simplest part. We know the hydrogen mass = 1.007825 u and for deuterium we have (from atomic tables): : ² D  =  = 2.01410 u. Then:

Q = [ 2(1.007825 u) – 2.01410 u] c²

Q = [ 2.01565  u – 2.015941u] c²

Q = [2.01565 – 2.01410] 931.5 MeV/u

Q = [0.00155] 931.5 MeV/u = 1.44 MeV

 

The effect of ongoing fusion reactions such as this,  means that the central core of the Sun becomes heavier and heavier, as more and more helium is produced. This despite the fact that the Sun as a whole is losing an amount of mass of roughly 4 x 10⁶ metric tones per second

 

Insight Problem:

If the atomic mass for helium 3 (³ He) is equal to 3.01603 u, then verify the other Q-values for the last two parts of the proton-proton cycle. A  simplified, compressed “net reaction”:

 ¹H + ¹H +¹H + ¹H ®  ⁴ He + Energy

Is sometimes used to evaluate the total energy released in the proton-proton cycle. Compute this energy and compare to the value obtained for the total energy released in the earlier example. Can you account for the difference?

Nuclear Fusion Reactions in the Aging Sun:

At some stage, when nearly the entire solar core is helium a new helium fusion phase will be ushered in (at higher temperature), such that the following reaction series, known as the ‘triple alpha’ process, kicks in: 

⁴He + ⁴He ®  ⁸Be + g  (- 95 keV)

⁸Be + ⁴He  ®  ¹²C + g  + 7.4 MeV

Here, the two alpha particles (helium nuclei) first fuse to give unstable beryllium and a gamma ray (g), with 95 keV energy absorbed. Then the beryllium fuses with a helium-4 to give carbon–12 plus a gamma ray and 7.4 MeV energy given off.

In this way a new cycle commences, leading to a heavier molecular weight core. Each successive burning phase, however, is less efficient than its predecessor, as can be seen by comparing the energy given off in the triple alpha process to the energy given off in the proton-proton cycle. The key thing to bear in mind in terms of a stable phase (i.e. ‘Main sequence’) star like the Sun is that it is in pressure-gravity balance. The outer gas pressure balances the weight of its overlying layers. Any condition likely to disrupt this balance is therefore of paramount interest.

The stable lifetime of the Sun depends on how long before it consumes ninety percent of the hydrogen in its core. Theoretical investigations using data from nuclear reaction rates and cross sections suggest the Sun’s Main Sequence lifetime at 8-10 billion years. Since it already has spent 4.5 billion of those years, there are anywhere from 3.5 to 5.5 billion years remaining. 

Once the triple-alpha process gets underway and the energy balance declines, the Sun will have to compensate for the lost energy to sustain any kind of balance. Thus, the Sun’s core must contract and convert gravitational potential energy into thermal energy.  Meanwhile, ignition of hydrogen burning in the Sun’s outer layers will create radiation pressure that forces the outer layers to expands. The Sun will then become a “Red Giant” and its new larger surface will be expected to engulf all the planets up to and including Mars.

 

Example Problem:

If the atomic mass of beryllium 8 (⁸Be) = 8.00531u, verify that the first part of the triple-alpha fusion process is endothermic and has the value given.

Solution:

 We have:

Q = [ 2(4.00260 u) –  8.00531 u] c²

Q = [ - 0.00011] 931.5 MeV = 0.102465 MeV = - 102.4 keV

Of course, not taken into account here is the gamma ray (g) which also comes off. Hence we will have:

(-102.4 keV) + (E (g)) = -95.7 keV

So that:

E (g) =   hc/ l = 6.7 keV

Is the missing energy of the gamma ray photon, with the difference factored in yielding 95.7 keV.

Aside: The Problem of the Coulomb Barrier in Solar Fusion

 The problem of the Coulomb repulsive barrier to solar nuclear fusion was first highlighted and explored by Prof. Martin Schwarschild in his excellent monograph 'The Structure and Evolution' of the Stars’  (Dover, 1958).

     Schwarzschild once calculated that the probability of any one proton fusion in the Sun’s core would ordinarily be  about once every 14 billion (14 x 10⁹) years. Since the universe itself is only 13.8 billion years old this means it could never occur unless another factor was present to enable it.

     The reason for this has to do with the Coulomb (electrostatic) repulsion between the potentially fusing H-nuclei. Thus, each proton, having (+) charge tends to repel any other proton within a discrete sphere or distance around it. (Recall from your basic physics, like charges repel, unlike attract - and that's what essentially obtains here)

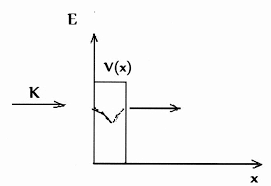
     In order for thermonuclear fusion to be realized, the Coulomb barrier must be overcome. Fortunately quantum mechanics allows for a certain non-vanishing probability that a particle (say proton) of kinetic energy K, can overcome a barrier of energy V ("barrier potential"), via the process of "quantum tunneling".

Note that tunneling is a general feature of low mass systems, such as single proton (H) states.

Consider a deBroglie (matter) wave arising from a single proton (p+) of form:

U(x) ~ sin(kx)

Where x is the particle's linear displacement (e.g. in 1-D) and k, the wave number vector(k= 2π/l), where l  denotes the wavelength.

    Though the associated kinetic energy K < V (the barrier "height") the wavefunction is *non-zero* within the barrier, e.g.

U(x_b)~ exp(- cx)

So, visualizing this behavior as shown below: 

                        Tunneling through Coulomb barrier potential  to allow nuclear fusion

 With the "barrier" at height V, so we can visualize the particle of lesser energy K, moving from the left side of the E-axis "tunneling" through to the right side where it may have wave function, U(x) ~sin (kx + φ), where φ denotes a phase angle.

    Note that if the barrier is not too much higher than the incident particle energy, and if the mass is small, then tunneling is significant.

    It's important here to point out that the penetration of the barrier is a direct result of the wave nature of matter. In effect, this wave nature - which is uniquely quantum mechanical in origin- allows a higher energy barrier to be penetrated by a lower energy particle, something totally without parallel in classical, Newtonian physics!

    Even given tunneling, an "offset" is required to reduce the low penetration probability , since clearly the Sun and other stars are shining by fusion.

     This 'offset' arrives via enormously high density of protons, e.g. in the core, which: i) increases the probability enormously, since so many more protons are in extremely close proximity, and (ii)enhances temperatures to the point they can be sustained, and continue - thereby building up other fusion reactions to finish the initial one.

   The idea here being that a particle of relatively low incident energy (of kinetic energy K, say) can actually penetrate a higher potential energy barrier, say of energy V(x) > K. Note that the penetration of the barrier is a direct result of the wave nature of matter! (The matter wave form changes in the process of transmission through the barrier, say from an exp(-ikx) function to a sin (kx + f) where f denotes phase angle). In effect, this wave nature - which is uniquely quantum mechanical in origin- allows a higher energy barrier to be penetrated by a lower energy particle, something totally without parallel in classical, Newtonian physics! Note that if the barrier is not too much higher than the incident energy, and if the mass is small, then tunneling is significant.   It was insights such as this that paved the way to apprehending how much subtler nature was than hitherto realized, and how many more technological advances could be achieved when the wave nature of matter was factored into designs. 

The Quantum Treatment of the Deuteron.

The deuteron is perhaps the most basic nuclear system to confront. As we know the deuteron consists of one proton, one neutron and the electron – with the first two comprising the nucleons.

To proceed, we write the usual Schrodinger equation for the hydrogen atom but let F and Q = const. so that their derivatives are zero. Then, substitute in the reduced mass:

m’=   m _n m _p/ (m _n + m _p)

So we obtain the new form of the Schrodinger equation:

1/r² d/dr (r² dR/dr)  + 2m’/ ħ²  [E – V] R = 0

This can be further simplified by letting:

U(r)  = rR(r)    which results in the equation:

d²U/dr²  +  2m’/ ħ²  [E – V] U = 0

In this equation we find that V, the potential, has two values:

V = - V_o and  V = 0 outside the well. The diagram below shows how we are treating the deuteron in terms of the function V(r).

              The potential well associated with the  deuteron 

There are then two solutions we can designate:

i) u _I for r   <   r _o and 

ii) u _II for r   >   r _o

Inside the potential well:

d² u _I /dr²  +  2m’/ ħ²  [E + V_o] u _I = 0

and we let:   a²  = 2m’/ ħ²  [E + V_o]

so that: 

d² u _I /dr²  +  a²  u _I = 0

For which we can show:

u _I    = A cos (ar)  + B sin(ar)

Since R = u/ r  the cosine solution must be discarded, lest we get an unwanted infinity. This leaves:

u _I    =   B sin(ar)

Outside the potential well  V = 0 so that:

d² u _II  /dr²  +  2m’/ ħ²  [E]  u _II = 0

Let:

b²  = 2m’/ ħ²  [- E ]

Since the total energy of the neutron is negative, i.e. being bound to the proton.  Then:

d² u _II  /dr²  -  b² u _II = 0

Which can be shown to have the solution:

u _II   = C exp (-br) + D (exp(br))

For consistency we demand u ® 0 as r ®¥, so D = 0 and:

u _II   = C exp (-br)

For continuity at r  =   r _o  and  u _I  =  u _II  :

B sin(ar)  =  C exp (-br)

Thence:

du _I /dr = d u _II  /dr Þ  aB cos (a r _o) = -bC e^{-b r o}

Now, divide the solution on the left side by the one on the right side, e.g.:

a B cos (a r _o) /   -b C e^{-b r o}

so:

tan (a r _o)  = -  a/b

In effect, the deuteron problem cannot be solved analytically, only graphically.

Quantum Numbers for Deuteron:

Since there are two particles, each with intrinsic spin ½   in the deuteron, the total intrinsic spin angular momentum can only have the values: S = s1 + s2 = 0 or 1.   The orbital angular momentum quantum number, L (describing the motion in space of the proton and neutron relative to each other) can assume the values L= 0, 1, 2 (i.e. S, P, and D states).

The total angular momentum of the deuteron has been measured and the total angular momentum quantum number J has been found to be 1. This must be the vector sum of the orbital angular momentum (L) and the total spin momentum (S).

Suggested Problems:

1) Calculate the wavelength of the gamma ray photon (in nm) which would be needed to balance the endothermic part of the triple –alpha fusion equation. (Recall here that 1 eV = 1.6 x 10 ^-19 J)

2) Verify the second part of the triple-alpha fusion reaction, especially the Q-value. Account for any differences in energy released by reference to the gamma ray photon coming off and specifically, give the wavelength of this photon required to validate the Q.

3) The luminosity or power of the Sun is measured to be L = 3.9 x 10²⁶ watts.  Use this to estimate the mass (in kilograms) of the Sun that is converted into energy every second. State any assumptions made and reasoning.

4) a) Show that u _I    = A cos (ar)  + B sin(ar)

Is  a solution of the reduced Schrodinger equation for the deuteron:

   d² u _I /dr²  +  a²  u _I = 0.

b) Show why the cosine solution needs to be discarded.

---

[1] See, e.g. Physics Today: Reports, April, 1995, p. 19.