TEACHING ALGEBRA II THE RIGHT WAY! USING APPLICATIONS!

According to the author of the HARPERS piece ‘Wrong Answer’, one gripe of Algebra II students is the ‘bait and switch’ tactics often used in their textbooks. The author cites a caption introducing Chapter 8 of the Algebra II Common Core text which displays a Basilisk lizard racing across the surface of a body of water – and there’s a hint (in the caption) of applying algebra to find the “surface tension” and application  – but nothing manifests. It’s a dead end!

The author, Nicholson Baker,  then exposes the scam:

“There’s nothing about surface tension or walking on water in Chapter 8, and indeed the caption would puzzle an expert on reptilian locomotion- since basilisk lizards don’t actually rely on surface tension to run on water. They’re like heavy striders”

He then goes on to explain the real physics, which attributes the lizards’ water skimming ability to “relying on the momentary inertia of the boluses of water beneath its long toed feet.”  In other words, certain discrete semi-separate masses of water (boluses) possess the property of inertia (resistance to displacement) when the reptile scampers over them – thereby allowing it to appear to skim the surface of the water if fast enough. But again, no algebra is shown to be applied.
 

Instead of teaching slavishly (and abstractly – i.e. via formal definitions), to a text, why aren’t various applications emphasized to really get students engaged? In this and two more blogs I will show a variety of ways to apply algebra to drum up of the interest of Algebra II students.  Each application requires only a passing or basic introduction to certain algebraic principles without going hog wild into abstraction, i.e. trying to get a kid to differentiate between continuous and non-continuous rational functions. In the case of an applications –based course, the question of whether functions employed are continuous will arise naturally – say in the course of discussions, or the applications.

 

 

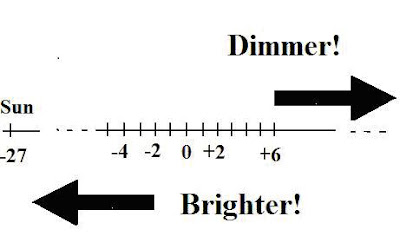
1. Application to the Number Line:
 

One of the foremost concepts any student of algebra needs to master is the number line. There have been various ways to present it, but the most sterile is the teacher simply drawing a boring line on a blackboard and filling in numbers - positive and negative- at regular intervals. A better way is to introduce an immediate application, which demands the use of such numbers - say the stellar magnitude scale shown above.

 

 

If the students are told there is a way to tell the brightness of one star from another, they ought to immediately become curious. You then let them know the brightest stars are assigned negative numbers and the less bright positive ones. A class exercise would be to mark out an extended magnitude scale, say from (-26.5) at one end, to maybe +10 or +15  at the other. You can then use a star atlas to write the stellar magnitudes on the board - or on whatever medium is applicable - and let the kids fill them in.

 

 2. Kinematic applications:
 

Number line too boring?

 

Then one can really get into the 'nitty gritty' with the application to kinematics and dynamics. In this case, the motion of some object, say motor vehicle, is recorded on a distance - time or other (velocity v. time) graph, such as shown below and the results interpreted.

The top graph gives the displacement s in terms of the time as: s = 2t. The bottom graph gives the velocity based on this motion, which will be: v = s/t = 2t/t = 2, say in meters per second. Since there is no initial velocity, u = 0, then (v – u)/ t = 0 and the slope the v-t graph is zero. Meanwhile, the graph of the s-t graph (top) has constant slope. In either of these instances one can infer there is uniform motion and hence Newton’s 1^st law of motion applies.

 

 

 The basic equations of kinematics can then be derived or given, allowing all sort of interesting problems to be worked out. These equations include:

 

 

1) v = u + at

 

 

which relates the final velocity to u, the initial velocity and then to the acceleration a and time it is in motion, t.

 

2) s = ut +  ½ at²

 

This relates the distance traveled to the initial velocity u, the time t, and any acceleration a, If the initial velocity u = 0 then, s = ½ at²

3) v²  =  u²   + 2as
 

A different form relating final velocity to initial velocity u, and distance covered, as well as acceleration.  Remember, that when one moves on to calculus, the primary bugbear of all students is algebraic manipulation (say using partial fraction decomposition),  not recalling continuous and discontinuous functions and their properties.  A good exercise for students is to change the subjects for the different kinematic equations, which the teacher can propose for different circumstances.

 

For example, take equation (2). Now, apply it to a falling body, say a rock, dropped from a tree 20 m high. Then we know s = 20 m, and the initial velocity u = 0. So, how long it will it take to reach the ground? You need to solve for t, the time. (You can take g = 10 ms^-2  to keep it simple, or use 9.8 ms^-2 .)

 

 

In the case of equation (3) maybe a car initially moving at 30 m/s brakes to 10 m/s and does so in two seconds. How would you find the deceleration a? Would you need more than one kinematic equation to find it?

 

 

Application problems:
 

 

1) A car moves at 10 m/s for a period of 5 seconds then slows to 5 m/s for the next 10 seconds. Draw a graph showing the complete motion. What is the speed of the car after 2.5 seconds? What is its speed after 8 seconds? What is the total distance covered over 15 seconds? Over the first 5 seconds?

 

 

2) A go Kart starts off with an initial uniform velocity of 2 m/s for 5 s. It then accelerates to 3 m/s in 1 second and sustains that for 3 seconds. What is the distance it covers?

 

3) A car is traveling along a level road at 50 km/h, then it speeds up to 80 km/h over a period of 5 minutes. Find the acceleration in m/s/s and the distance covered in the time, in m if it maintains the final velocity for 1 minute. (Take 1000 m = 1 km, 1 h = 3600 s)