1)The student will need to understand that the group of translations required will be for a type of transformation that takes each point in the graph (in this case y = x +1) and slides it the same distance in the same direction, in this case to y = x + 3. Considering a flat 2-d plane he will want to translate points (x,y) to: (x+a,y+b)(x+a, y+ b), where a = -2 and b = 0.
Or in matrix form:
(3,4) -> (1, 4)
(2, 3) -> (0, 3)
(1,2) -> (-1, 2)
(0, 1) -> (-2, 1)
(-1, 0) -> (-3, 0)
(-2, -1) -> (-4, -1)
We see in each case b = 0, a =
-2 But on doing even a few
such mappings it should occur to the savvy reader that it isn’t limited to
integer values. For example, let x = 2.3111 then x + a = 0.3111, or let x = ½, x + a =
½ +(-2) = -3/2 and so on. In
effect, one has an infinite set.
Meanwhile, y -> (y + b) remains the same for any (x+ a), (y + b)
To obtain his desired parallelogram the student needs to see that there must be a boundary or termination point to the mapping to avoid an infinite set, i.e. extending beyond the given domain and range. Then he needs to set out limits for x->x+ a:
{x,y : x->x+ a : x< 2, x +a > -6}
2) Rem. Coordinates have been transformed to different origin, viz.
So displaced origin is now at:
(x’, y’, z’) = (x+0, y+6, z+0), =
(0, 6, 0)
In original system Q is at:
x= a= 4, y= 0, z = c= 2,
So from (0,0, 0) Q position
was: (4, 0, 2) and length of Q =
Ö (4) 2 + (2) 2 ) = Ö (20) = 4.47
But in new system,
coordinates are: (x’ = 0, y’ = 6, z’ = 0)
And length of Q =
Ö (4) 2 + (2) 2 +
(6) 2
= Ö (56) = 7.48
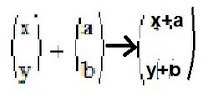

No comments:
Post a Comment