A Look At Basic Solar Dynamo Theory

 Sunspots exhibit a definite periodicity but in addition do not occur randomly on the solar surface but are instead concentrated in two distinct latitude bands best seen in what is called a “butterfly diagram”, e.g.

Here we can see that the sunspots are confined mainly between heliographic latitude 30 N and 30 s, in a wide interval of time from before 1880. Note each “wing” edge to the left shows the beginnings of each cycle – where sunspots first appear. Following the “wing edge” downwards one sees that spots migrate toward the solar equator where they disappear until the next minimum.

 This form of equatorial migration or motion in a given cycle is known as Sporer’s Law. This suggests an underlying flow or wavelike propagation that may be tied to shear variability near the solar tachocline, e.g. 

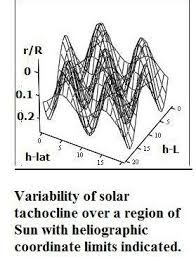
                              Representation of shear variability near the solar tachocline.

In the diagram, the axis defined h-lat denotes the heliographic latitude and h-L the heliographic longitude, while the vertical axis denotes the fraction of solar radius defined from “0” or the tachocline.  The peaks and troughs can then be interpreted as mammoth “shear waves” which will affect the meriodonal flow and could possibly have been responsible for the long delay of sunspot emergence in solar cycle 24.

 For their part, the torsional oscillations tend to occur about 1000 kilometers below the Sun's surface (photosphere) but we have few instruments that can actually probe that deeply.  Clearly there is a case to be made for solar "sounding" which might help to discriminate between the classical (e.g. Babcock-Leighton) dynamo theory and new ones involving "shallow" dynamos.

In classical dynamo theory we are looking at the process by which the solar magnetic field is generated through a combination of rotation and convection. We refer to the two parts of the dynamo process the a-effect and w- effect.  In the latter, the shear flows (such as visible in the tachocline diagram) are able to stretch the photospheric magnetic field lines in the direction of the shear while in the former, helical flows are able to lift and twist field lines into orthogonal planes.

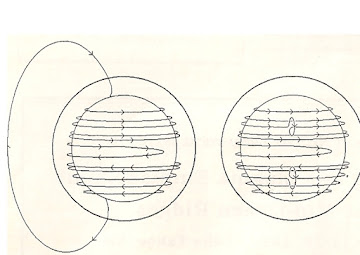
  These two complementary aspects and effects (defined as a and w)  are illustrated below :

Comparison of the a - w  dynamos (a  on right)

Note the expansion and direction of the reference field line for the w- effect,  and conversely the compressed nature and field line directions for the a-  effect.  Given below are the four primary equations pertaining to magnetic induction :

       The basic equation for solar dynamo theory is given by (1) which is constructed from Maxwell’s equations and the solar form of Ohm’s law. See e.g.

• Basic Solar Electrodynamics Revisited

 Where B is the magnetic induction, v is the velocity and h is the magnetic diffusivity. It should be noted that in the B-v paradigm, because of the the rapidly fluctuating values, we employ a “mean field” approach whereby B and v are separated into mean and fluctuating parts. Following this prescription and taking the average of the cross product of fluctuating velocity and magnetic induction, one arrives at (2)  Which states that the averaged cross product is proportional to the magnetic induction and its curl, with the overbar on the former indicating its averaged value. The constant a is proportional to the helicity in the fluctuating velocity field.  The constant b is proportional to the  eddy diffusivity.

 Using cylindrical coordinates (r,  q,   f) the equation (1) can then be written in terms of the azimuthal component of the magnetic induction and the poloidal component , or B _p = (B_r ,  B _j)  =   Ñ X A, where A is the vector potential.  This yields the  pair of coupled equations(3, 4). Where U is the mean fluid velocity consisting of a meriodonal flow, U _p  and a differential rotation, U_j. If one neglects the former, then equation (4) shows that the poloidal field is produced by the a - effect.  

 Conversely, equation (3) shows the toroidal field is produced by both the a - effect and the w- effect where the   B _p field is stretched by differential rotation. It is important to note that the relative strength of the terms determines the properties of the particular dynamo.

 For example, if differential rotation magnitude is much less than the a - effect one can drop the w- effect from equation (3). Conversely, if the differential rotation is much greater than the a - effect, then the a - effect term is dropped from the same a -w dynamo equation. These dynamos generate shear waves that propagate at right angles to the shear flow as depicted in the tachocline model image.  

 Given all the variations on the basic dynamo effect, including the a² - w dynamo, it is perhaps not surprising that novel or emergent phenomena can manifest. For example,  ephemeral photospheric regions (EPRs) might be the first phenomena to be accounted for in advance of actual sunspots  and tied to certain dynamo actions. They are often portrayed as "inverse ion hurricanes". As the name implies, EPRs are not very stable or long lasting, usually appearing as small pores, then vanishing in 1-2 days.

  A fully consistent shallow dynamo theory needs to present sufficient observational and numerical analyses to back up the supposition that a super-adiabatic temperature gradient is largest near the surface and a large sunspot can be supported by the associated latent energy through the reaction:

H + (energy) -> H+ + e(-) [ionization of hydrogen]

     Further research into this area is ongoing at a number of institutions and should soon be ready for publication in the Physics  arXiv.