One of the most fundamental astronomy areas, which also gave teachers and students doing CXC Astronomy fits, concerned the matter of relative and absolute brightness and stellar magnitudes. (Specifically, the stellar magnitude scale). Of course, it's always best to begin such a topic with prosaic examples.
I tended to use the simple, everyday example of comparing two light bulbs. Thus, if I have a 100 watt bulb and place it at 1 m, then what would its relative brightness be placed twice as far away? By the inverse square law for light (the intensity of a light source decreases as the inverse square of its distance):
(d1/d2)^2 = B2/ B1
Where in this case, d1 = 1 m, B1 = 100 w and d2 = 2 d1 = 2m. Then, it’s obvious one needs to find B2.
B2 = B1 (d1/d2)^2
But (d1/d2)2 = (1/2)^2 = ¼
Therefore: B2 = 100 w (¼) = 25 watts
What appeared to trip up many students was the inverse nature of the proportion (and for many others, the squaring of the distance term).
In the astronomical context, the student ought to be able to use the same method in applying the inverse square law to stars. But actually doing it proved to be the bugbear! For example:
Beta Crucis has an apparent magnitude of +0.8 and this is from 261 light years. Find its absolute magnitude.
The student is first given the basis of absolute magnitude as that apparent magnitude defined at a distance of 10 parsecs, and if there are 3.26 light years per parsec this means, 10 pc (3.26 ly/pc) = 32.6 light years. Then, for Beta Crucis:
(d1/d2) = 261 ly/ 32.6 ly = 8
Then:
(d1/d2)^2 = (1/8)^2 = 1/64
So:
B2/ B1 = 1/64
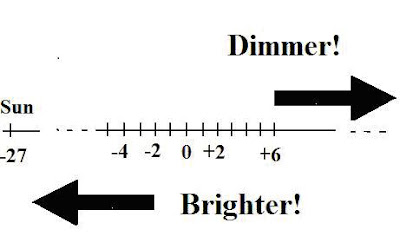
But in this case the object is being brought closer, so we want to find B1! Thus, B1= 64 B2. In other words, the star’s brightness at 32.6 light years is roughly 64 times more than its brightness at 261 light years which converts to a magnitude difference of: 4.5. (See Fig. 2 for a stellar magnitude scale - with the Sun at the extreme left or brightest end, with an apparent magnitude of (-27).
So the new magnitude would be: (0.8 – 4.5) = -3.7.
That is, we locate +0.8 on the scale, then march off 4.5 units on it in direction of increased brightness.
Ah, the magnitude scale and magnitude difference, introducing a logarithmic scale on top of the ratios! More headaches!
The layout of the scale is arithmetical, like the algebraic number line, but when related to brightness one obtains ratios not differences. And these ratios are based on a logarithmic relation. For example, the apparent magnitude of the Sun makes it apparently the brightest object in the sky. But this is only because it is at 1 A.U. distance. IF “moved” to 32.6 light years (the standard candle distance to obtain absolute magnitude) then one obtains +4.8 magnitude.
Thus, its real magnitude in terms of the absolute standard (absolute magnitude) makes it somewhat dim.
The basic gist of the scale is that every 5 increments (UNITS) in magnitude difference translates into 100 times difference in brightness, because each succeeding magnitude is different from the earlier one by 2.512 times, since:(2.515)^5 = 100. Thus a star of +1 magnitude is 100 times brighter than a star of +6 magnitude on the scale, since (6 – 1)= 5.
Problems:
(1) (a) Using the scale in Fig. 2 as a basis construct a simple stellar magnitude scale ranging from (-10) to (10).
i)Sirius has a magnitude of (-1.4), mark it on the scale and label it.
ii)Castor has a magnitude of (+1.6) mark its place on the scale and label.
iii)Sigma Draconis has a magnitude of (+4.7), mark and label it.
iv)Zosma has a magnitude of (+2.55), mark in and label it.
(b)Which is brighter, Sirius or Castor, and by how many times? Which is brighter, Zosma or Sigma Draconis and by how many times? A new star Alpha Stellaris is discovered which is found to be 15.6 times brighter than Sirius. Locate its approximate position on the scale and label it. Estimate how many times brighter this new star is than Sigma Draconis.
(2) One of the stars shown on the star map of Fig. 1 is Regulus in the constellation Leo. It has an apparent magnitude of (+1.35) and an absolute magnitude of (-0.6). Using this information only, estimate its actual distance from Earth.
(3) The Sun's absolute magnitude is +4.8. How much farther would it have to be from us to appear with that magnitude in the night sky? (The Sun's mean distance from us currently is 150 million kilometers for which the apparent brightness is (-27).
(4) Two stars in the same constellation are named Alpha and Gamma. Both have the same absolute magnitude. Alpha is at a distance of 32.6 light years and has an apparent magnitude of +0.8. Gamma is at a distance of 261 light years.
a)Using the inverse square law of light, estimate how many times Gamma is dimmer than Alpha.
b)Based on the stellar magnitude scale, estimate Gamma’s apparent magnitude.
No comments:
Post a Comment