Solutions to Simple Astronomy Problems (3)

We now examine the solutions to the last set of simple astronomy problems. The problems again are given first for reference, then their solutions.

Problems (3):

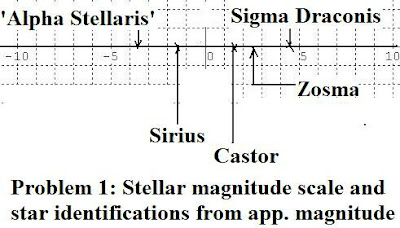
(1) (a) Using the scale in Fig. 2 as a basis construct a simple stellar magnitude scale ranging from (-10) to (10).

i)Sirius has a magnitude of (-1.4), mark it on the scale and label it.
ii)Castor has a magnitude of (+1.6) mark its place on the scale and label.
iii)Sigma Draconis has a magnitude of (+4.7), mark and label it.
iv)Zosma has a magnitude of (+2.55), mark in and label it.

(b)Which is brighter, Sirius or Castor, and by how many times? Which is brighter, Zosma or Sigma Draconis and by how many times? A new star Alpha Stellaris is discovered which is found to be 15.6 times brighter than Sirius. Locate its approximate position on the scale and label it. Estimate how many times brighter this new star is than Sigma Draconis.
---

Solution:

The constructed magnitude scale is shown with the stars identified by their apparent magnitudes, including 'Alpha Stellaris' (from part (b))

As to the answers for part (b):

Sirius is at m = (-1.4) and Castor at +1.6 so the magnitude difference is:

[1.6 - (-1.4)] = 3.0

so the difference in brightness (brightness ratio of Sirius to Castor) is:

(2.5)^3 = 15.6 times

Alpha Stellaris is 15.6 times brighter than Sirius therefore (from the previous working) it will be three units of magnitude brighter, hence will be at:

(-1.4) - 3.0 = -4.4 magnitude

Relative to Sigma Draconis, Alpha Stellaris would be:

+4.7 - (-4.4) = 9.1 magnitudes brighter or

(2.5)^9.1 = 4,180 times brighter



(2) One of the stars shown on the star map of Fig. 1 is Regulus in the constellation Leo. It has an apparent magnitude of (+1.35) and an absolute magnitude of (-0.6). Using this information only, estimate its actual distance from Earth.
----
Solution

Regulus' magnitude (by def. of absolute magnitude) would be -0.6 at 10 pc. Therefore, being (+1.35) it is actually further away than 10 pc. The magnitude difference is:

+1.35 - (-0.6) = 2.95

or a brightness ratio (b/b') = (2.5)^2.95 =14.9

but: d'/d = (b/b')^2

so d' = (14.9)^½ d = 3.86d

therefore d' = 3.86 x 10 pc = 38.6 pc (actual distance) est.


(3) The Sun's absolute magnitude is +4.8. How much farther would it have to be from us to appear with that magnitude in the night sky? (The Sun's mean distance from us currently is 150 million kilometers for which the apparent brightness is (-27).
---
Solution

First obtain the difference in magnitudes:

(+4.8 - (-27) = 31.8 units of magnitude.

Then the brightness ratio is:

(2.5)^31.8 = 4.5 x 10^12

But the distance is related as the inverse square, so:

(d/d') = 1/(4.5 x 10^12)^1/2= 2.12 x 10^6

so the Sun would have to be about 2.1 million times farther away (e.g. 3.1 x 10^14 AU)

(4) Two stars in the same constellation are named Alpha and Gamma. Both have the same absolute magnitude. Alpha is at a distance of 32.6 light years and has an apparent magnitude of +0.8. Gamma is at a distance of 261 light years.

a)Using the inverse square law of light, estimate how many times Gamma is dimmer than Alpha.

b)Based on the stellar magnitude scale, estimate Gamma’s apparent magnitude.
--
Solution

Part (a) just requires taking the distance ratio:

d2/d1 = 261 LY/ (32.6 LY) = 8.0

so by the inverse square law, the brightness of Gamma (being eight time more distant) must be 1/64 of Alpha’s.

Part (b) is simply applying the logarithmic features of the stellar magnitude scale. Again, I remind readers that every unit magnitude difference (arithmetic) is equal to a brightness ratio of 2.5 times. Thus, to obtain the apparent magnitude of Gamma, we need to solve:

(2.5)^x = 64 or x (log 2.5) = log (64)

Then: x(0.39) = 1.80 and x = (1.80)/ 0.39 = 4.6

Which meant Gamma’s apparent magnitude was:

m = (0.8) + 4.6 = +5.4