More Linear Algebra: Finding Orthonormal Bases

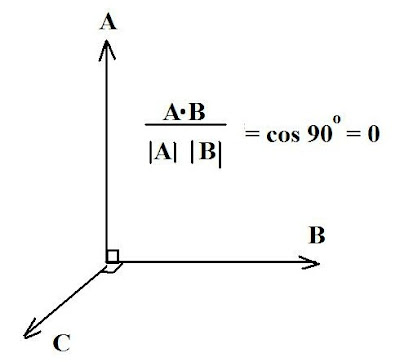
Many students who take linear algebra courses at university, often forget they were likely exposed already to many of its concepts and principles ...but in a different guise or a different subject. Take, for instance, the concept of an "orthonormal basis". The term sounds esoteric but many would have encountered it before either in general physics or in advanced (AP) physics courses taken in high school. This would be in conjunction with the dot product of vectors, such as illustrated in Fig. 1.

Basically, in some Euclidean (straight line, 3D) system of coordinates, two vectors are considered orthogonal if their inner product is zero, as shown. The geometric properties hererely on the basis being orthonormal, i.e. composed of pairwise perpendicular vectors with unit length. Thus, in the figure shown, vectors A and B meet this condition (and the computation is shown for the vectors A, B) as do the vectors B and C. Then the vectors A, B, C meet the condition for an orthonormal basis. There are proofs available but those are beyond the scope of this blog.

Now, in applications of this concept, what the student is usually asked to do (say in his linear algebra course) is find an orthonormal basis for a "subspace" of R^3 (e.g. applied to a Cartesian space of three dimensions) which is generated by specified sets of vectors.

Example:

Find an orthonormal basis for the subspace of R^3 generated by the vectors (1, 1, -1) and (1, 0 ,1).

We let A = (1, 1, -1) and B = (1, 0, 1)

The orthonormal basis for A is just:

A/ ‖A ‖ = (1, 1, -1)/ {1^2 + 1^2 + (-1)^2} =

(1, 1, -1)/ [3]^½

The orthonormal basis for B is:

B/ ‖B ‖ = (1, 0, 1)/ {1^2 + 0^2 + (1)^2} =

(1, 0 , 1)/ [2]^½


Of course, the beauty of linear algebra is that it can be generalized to Euclidean spaces beyond the mundane 3, hence we can look at subspaces in R^4, generated by sets of vectors (v1, v2, v3, v4).

Example:

Find an orthonormal basis for the subspace of R^4, generated by the vectors:

A = (1, 2, 1, 0) and B = (1, 2, 3, 1)

For A we have the orthonormal basis:

A/ ‖A ‖ = (1, 2, 1, 0)/ {1^2 + 2^2 + 1^2 + 0^2} =

(1, 2, 1, 0)/ [6]^½

For B we have:

B/ ‖A‖ = (1, 2, 3, 1)/ {1^2 + 2^2 + 3^2 + 1^2} =

(1, 2, 3, 1)/ [15]^½



Problems:

(1) Find the orthonormal basis for the subspaces of R^3 generated by the vectors:

A = (2, 1, 1) and B = (1, 3, -1)

(2) Find the orthonormal basis for the subspaces of R^4 generated by the vectors:

A = (1, 1, 0, 0)

B = (1, -1, 1, 1)

C = (-1, 0, 2, 1)

(3) Find an orthonormal basis for the subspace of the complex space C^3 generated by the vectors:

A = (1, -1, i)

and

B = (i, 1, 2)