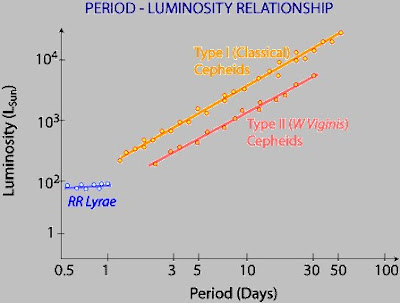
Graph showing the period-luminosity relationship for Type I and II Cepheid Variables, and RR Lyrae stars.
Technically, it would take a short book to document in detail all the methods of measuring stellar and celestial distances with any degree of completeness. What I'll do in this blog is give a snapshot view of some of the basics for a few of the major methods, used for different distance scales.
The most basic and intuitive method for measuring a star's distance employs elementary trigonometry. It is called the "parallax method" because it uses the phenomenon of "parallax".One can get a simple idea of this by holding an index finger at arm's length- then looking at it with only the right eye open, then only the left. What you'll see as you do this alternatingly - is the visible shift of your index finger against the background. Say from one part of your book shelf to another. (A very tiny shift.)
The angle subtended between the different background points, with respect to your nose ("vertex" of the resulting triangle), say- is the "parallax angle".Now, let's generalize this to stars, using the diagram below - which I hope comes out reasonably well in the response:
(E1) x
-------------------d--------------------O (star)
(E2) x
Here, the points E1 and E2 represent Earth at two opposite points of its orbit around the Sun. The star indicated is the one for which the distance(d) is sought. Using photographs of the star taken at the points E1 and E2, we can measure what is called the angle of parallax p.The solution for the distance can be obtained from:
d = r/ tan(p)
that is, equal to the radius (R) of the Earth's orbit (equal to 1 A.U. or astronomical unit = 93 million miles = 1.5 x 10^11 meters) divided by the tangent of the angle p. (which will be a very, very small angle).The tangent is a function which denotes a ratio of lengths for a right triangle. In this case, the tangent of the angle p is defined:
tan(p) = opposite/ adjacent = R/d
that is, the side (radius = R) opposite the angle, divided by the side (d = distance to star) adjacent to the angle (d). Using algebra, one then makes d the subject, which means solving for it.
It can be shown, from the above, that for an angle p = 1" (one second of arc, or 1/3600 of a degree! (Bear in mind 60' = 1 deg and 60" = 1' or 1 minute of arc) the resulting d = 206, 265 A.U. or astronomical units (206, 265 x 1.5 x 10^11 m).
The name we use for this particular distance is the parsec and doing the math (tedious, but possible) shows the distance turns out to be:
1 parsec = 3. 26 light years.
Now, given this relation, it follows that any proportionate decrease in the angle p allows one to work out the resulting distance! Thus, if p = 0.5" then d = 2 parsecs or 6.52 Ly, if p = 0.25" then d = 4 parsecs or about 13 Ly and so on, and so forth. Thus it was found that even the nearest stars were light years distant - using the simplest conceptual method available. The first successful parallax measurements - so far as we know - took place around 1838, when Friedrich Bessel (Germany), Thomas Henderson (Cape of Good Hope) and Friedrich Struve (Russia) detected the parallaxes of the stars 61 Cygni, Alpha Centauri and Vega, respectively.
No one knows who "first" used it. Parallaxes have been measured for thousands of stars. However, for barely 700 are the angles (p) large enough (about p = 0.05" or more) to be measured with a precision of 10% or better. (Which means the resulting distances will have the same order of uncertainty).
Most of these measurable stars are within 20 parsecs or around 66 light years. Clearly, other methods are needed to measure larger distances.Among these is the method of Cepheid variables. These are a special type of star for which the brightness changes as its surface swells (expands) then contracts. In 1912, a period-luminosity relationship was discovered for these stars, by Henrietta Leavitt, an astronomer at Harvard College Observatory. Most of these were in the satellite galaxies (to our own) known as "the Small" and "the Large" Magellanic Clouds.Leavitt's now famous "law" for period-luminosity (relating the time to vary to intrinsic brightness) is found in many astronomy books.
Employing this law enables us to use a kind of a "standard candle" to measure distance - based on the principle of the inverse square law for light (e.g. if you have two light sources, say two 100w light bulbs, and place one 5 feet away, the other ten feet away, the more distant one - which is 2x further- will have 1/(2)^2 or 1/4 the apparent brightness of the one closer to your eyes. Thus, it will "appear" as a 25 w bulb by comparison!)
What one sees is the apparent magnitude of the stars plotted against the logarithm of their period (in days). Thus, there is a relation between the apparent magnitude of the star and period of its light curve.Now, since there is a direct relation between apparent and absolute magnitude (the absolute magnitude of a star is just its apparent magnitude from the same standard distance of 10 parsecs or 32.6 light years) there must also be a direct relationship between a (Cepheid) star's period and absolute magnitude.
Thus, if a given set of Cepheids can have absolute magnitudes assigned to them, the relationship between their periods and absolute magnitudes acts as a distance measuring device. Entering into this is what is called the "distance modulus" (m - M) given as the difference between apparent magnitude (m) and absolute magnitude (M):
(m - M) = 5 log_10 (r) - 5
Here, r is the distance to be found. For example, say a star is found to have: m = +4.5, and M = +6.0 (meaning it is actually brighter in apparent magnitude than it really is).
We have:
(4.5 - 6.0) = 5 log_10 (r) - 5(-1.5) + 5 = 5 log_10 (r)3.5
= 5 log_10(r)
then: log_10(r) = 3.5/ 5 = 0.70
taking anti-logs:
r = 5.0 (parsecs)
Which is actually for the star 40 Eridani.
Now, in the case of Cepheids - to employ the P-L relation for any star, we need to first find a 'zero point' applicable (this is not easy by any means, and I don't intend to go into the technical details!) By choosing the correct "law" appropriate to the type of variable star observed (e.g. 3-day period, 10 -day period, 30-day period etc.) a value can be inserted for the absolute magnitude M.
Then we can again apply the distance modulus equation, as I demonstrated above, since we now have values for both m and M. Note that the Cepheid method is good for many stars in nearby galaxies (like the Magellanic clouds) or in star clusters. However, one must realize problems can arise - for example many of these Cepheids are in dusty regions of the Milky Way with some light lost by absorption - making them appear less bright than they'd normally be at that distance. Hence, if such anomalous Cepheids are used for finding a distance they'd give a skewed, erroneous result.At much larger distances, say for galaxy clusters - we make use of the so-called "Hubble relation" or law.
That is, Edwin Hubble first discovered that the galaxies are speeding away from us with velocities proportional to their red shifts. (This is in reference to the shift of observed, known spectral lines toward the red or longer wavelength region - disclosing movement away from an observer. This observation for multiple distant objects has revealed the "expansion" of the universe).
The red shift is given by:
z = v/c
where c is the velocity of light (300,000 km/s)
For example, if the H-alpha spectral line is found to redshift by 20% from its normal position (at 6563 Angstroms, where 1 Å = 10^-8 cm) we have:
0.2 = v/c or v = 0.2 c
In other words, its velocity of recession is two-tenths the speed of light, or 0.2 (300,000 km/s) = 60,000 km/s
The distance can then be found from the Hubble law:
v = cz = HD
where H is Hubble's constant, and D is the distance of the galaxy cluster or other object (e.g. quasar)
We believe that H = 100 km/ sec (Mpc ^-1)according to recent measures, so (using the example of the recessional velocity, v above):
D = v/ H = 60,000 km/s / [100 km/ sec (Mpc ^-1)]D
= 600 Mpc (Mega-parsecs)
That is, 600 x (10^6) parsecs = 6 x 10^8 parsecs
or 6 x 3.26 x 10^8 light years = 1.95 x 10^9 light years
Or, about two billion light years.
The preceding examples, starting with simple parallax- allow one to see that distance measurement (and technique) in astronomy is by no means straightforward. This is also possibly why it is difficult to get satisfactory answers, since there are so many different methods appropriate to differing distance scales. In addition, to understand each method, both mathematics, and a certain amount of physics (e.g. inverse square law for light, spectral line shifts etc.) enter at each point. Therefore, appreciation of the distance methods and their appropriate use, really depends on how much of the physics - and math - one is able to incorporate in order to ascertain for himself how it works.
No comments:
Post a Comment