
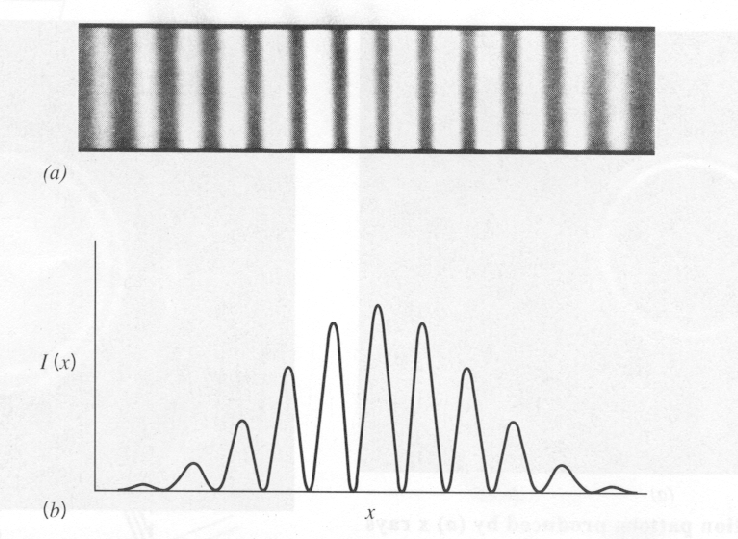
In the diagram directly above there appears a two-slit diffraction pattern and also an associated intensity pattern showing the relative light intensity for the pattern -obviously with the central portion amplitude above the rest.
David Deutsch's arguments on p. 44 of his monograph ('The Fabric of Reality") basically contend that:
"there is no intrinsic difference between tangible and shadow photons: each photon is tangible in one universe and intangible in all the other parallel universes"
In his representation on p. 41 (Fig. 2.7), we see a similar pattern to the one given above, along with an additional pattern in which the dark interference fringes are much wider. He infers that "something must be coming through the second pair of slits (bear in mind two, 2-slit arrangements are set up in sequence) to prevent the light from the first pair reaching X? But what? We can find out with further experiments."
After a lengthy bit of reasoning, including successive tweaking of thought experiments, Deutsch arrives at "shadow photons from a parallel universe". He infers (p. 44) for at least one arrangement "at least a trillion shadow photons accompanying each tangible one."
He also is careful to distinguish the respective properties: (ibid.)
"Thus, we have inferred the existence of a seething, prodigiously complicated, hidden world of shadow photons. They travel at the speed of light, bounce off mirrors, are refracted by lenses, and are stopped by opaque barriers or filters of the wrong color. Yet they do not trigger even the most sensitive detectors. The only thing in the universe that a shadow photon can be observed to affect is the tangible photon it accompanies. That is the phenomenon of interference. Shadow photons would go entirely unnoticed were it not for this phenomenon."
In light of the above, we now return again to the experience of Charlotte Moberly and Eleanor Jourdain in experiencing a time slip transferring them from the year 1901 to 1789. (Previous blog). Moberly described a flat and lifeless terrain in her report and most importantly declares: "There were no effects of light and shade, and no wind stirred the trees". What do we infer?
If there really were "no effects of light and shade" then it must mean that their surreal domain was in fact an inter-phased one for two parallel universes. In this domain we surmise that if they could have performed the sequential two slit diffraction experiment cited by Deutsch they'd have found instead a central large dark area and bright fringes. As opposed to a central bright region and dark fringes. In addition, we may infer this interphased domain was dominated by shadow photons over tangible ones but at different angles. This is why "everything suddenly looked unnatural, therefore unpleasant; even the trees behind the building seemed to have become flat and lifeless ".
It is important to reiterate here, that according to the standard multiverse theory (based on cosmic inflation), there are basically an infinite number of parallel universes. In the hyper-toroid geometry (graphic shown in the previous blog) these separate universes can be regarded as lines of longitude, since an infinite number of them can be fit around the circumference of the hyper-sphere. If say, one somehow for some reason briefly overlapped another, one would expect an interphase condition. This then would permit a time slip to occur but it would not be between times in the same universe (say for the Brit pair between the 1901 and 1789 Earth as we know it) but between TWO distinct parallel universes. That is, they'd have slipped from 1901 in this universe with the Earth as it exists therin, to another (parallel) universe with the Earth as it existed in 1789.
Let's now explore the dynamics more closely, using the diagram shown at the very top, for two spaces in algebraic homology:
T = S1 X S1
The first (space) is the circle all the way around the middle of the 'donut's body. The second (time) is the circle around a section of the donut itself. Here (diagram), the respective spaces (circles S1) define two dimensions for what we will call the global state space GL. Thus, we have:
GL = S1 X S1 = (SPACE) X (TIME)
The line marked 'Axis' defines the center of the toroidal space we are looking at. The important point is that the time cycle is mapped all along the (single) S1 cycle of space. The space cycle therefore defines all hyperdimensional cosmic time cycles that ever have, or will, exist. Evidently, there are an infinite number of such cycles, since an infinite number of points can be mapped onto the space cycle as well.
All cycles are identical in the infinite series (Σi Θi) but also different. Identical, since each cycle goes from 0 through 360 degrees, folding back on itself so that a particular beginning (Big Bang = 0) and ending (Big Crunch = 360°) for each universe occurs at one and the same point (0° = 360°). Hence the same initial and final coordinates apply to all cosmic cycles. Θ is thus a fixed dimension of the Young-model ‑hypertorus, much like time in the Minkowski universe. Indeed, in the hypertorus overview, any position can be fixed by two coordinates (φ, Θ) where the φ is used for space and Θ for time. In fact, since both are circles, it makes sense to assign them angles: one (φ) for space, the other (Θ) for time.
Consider now, the mapping for the phase space volume we called the global state space. It is the (topological) space of all possible times and all possible spaces, for all possible universes. Thus, it is an imaginary (in the mathematical sense!) space. Two possible events in this global state space might be designated:
Ξ = (φ, Θ) AND Ξ' = (φ',Θ')
By way of example, Ξ could be the assassination of Hitler, and Ξ' the event wherein Hitler escapes assassination. Either one is possible but not both simultaneously in the same cosmic cycle or universe! We already know we inhabit the cycle for which Ξ' holds, so the other (Ξ) cannot. The "pasts" are thus mutually exclusive, which further reinforces Hawking's "temporal censorship" postulate that one cannot go back and change the past.. The topological space of the hypertorus cosmos can therefore be represented by the global state space, a product of absolute hypertorus coordinate time (Θ) and 'all-space'(φ):
GL = Θ X φ
Now, the set of specific times t_i C Θ_i, and the set of specific 4-dimensional spaces R_i C φ_i, so the space of all local states, L is the product space of four dimensional spaces and specific times:
L = R X t
We now need to look at is how L and GL are related, and the space and time sets within them: L Ì GL That is, the local state space L is contained within the global state space GL, but can never be equal to it The same applies to the subsidiary spaces: R in relation to φ, and the specific times: t in relation to Θ.
For example, for Θ, there is some spatio-temporal matrix M with generalized dimensional indices {x0, x1, x2, x3}. No one of these is 'time' specifically and uniquely. Rather, "time" arises when the three space indices have been assigned (i.e. if φ= {x1, x2, x3}, then Θ = {x0}. In effect, as S. Auyang observes: "the structure M is too primitive to confer special meaning on the time dimension. M is not in time, it is all times." (How is Quantum Field Theory Possible?, Oxford University Press, 1995, p. 169). By contrast, 't carries the load of temporal significance'. (Note here that when the 4 dimensional indices for each parallel universe are defined, then it becomes possible to more rigorously separate the parallel universes, i.e. in terms of their respective physical constants, specific times of origin, and duration.)
"Time" then is by no means as straightforward as often assumed, especially if one can plausibly have both time and space uncertainty - i.e. the Heisenberg Indeterminacy principle applicable to each. If this be so, then one can conjecture unusual conditions in which both space and time indeterminacy for two adjacent parallel universes allow for brief interphasing. If a sentient person, human, happens to be at such a location when this indeterminacy of space and time occurs, he can experience a "time slip".
Again, we cannot say the person or persons are really "going back in time". Instead, only that they have transitioned from a current coordinate Θ1 in one universe to Θ2 in other. While Θ2 appears to be "backward" in time by the reckoning of the person at Θ1 it is not really in relation to their own universe.
Part 3: Can I do a time slip to take me to the Kennedy assassination in any universe?
No comments:
Post a Comment