Selected Questions- Answers From All Experts Astronomy Forum(Stellar Brightness- Magnitude Scale)

Question: Can you please explain how stellar brightness is discerned and especially the basis fo rthe stellar magnitude scale which still mystifies me?

Answer:

The easiest way to grasp stellar brightness is to use a simple analogy. Say I have  a 100 watt bulb and place it at a distance of 1 m, then what would its relative brightness be if placed twice as far away? By the inverse square law for light (the intensity of a light source decreases as the inverse square of its distance):

(d1/d2)² = B2/ B1

Where in this case, d1 = 1 m, B1 = 100 w and d2 = 2 d1 = 2m. Then, it’s obvious one needs to find B2.

B2 = B1 (d1/d2)²

But (d1/d2)²  = (1/2)² = ¼


Therefore: B2 = 100 w (¼) = 25 watts

In the astronomical context, one ought to also be able to use the same method in applying the inverse square law to stars. 

For example, say you are given this problem:  Beta Crucis has an apparent magnitude of +0.8 and this is from 261 light years. Find its absolute magnitude.

You'd first need to know  the basis of absolute magnitude (M abs) as that it is just  apparent magnitude (m) defined at a distance of 10 parsecs. If there are 3.26 light years per parsec this means, 10 pc (3.26 ly/pc) = 32.6 light years. Then, for Beta Crucis:

(d1/d2) = 261 ly/ 32.6 ly = 8

I.e. Beta Crucis must be eight times nearer for taking M (abs).

Then (by inverse square law for light):

(d2/d1)²   =  (8)² = 64

So:

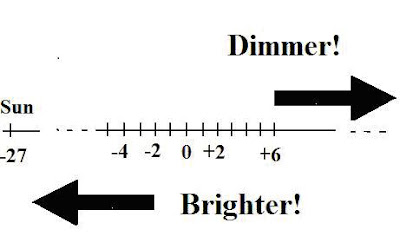
Thus, B1= 64 B2. In other words, Beta's brightness at 32.6 light years is roughly 64 times more than its brightness at 261 light years . This converts to a magnitude difference of: 4.5. (See the diagram below for a stellar magnitude scale - with the Sun at the extreme left or brightest end, with an apparent magnitude of (-27):

The layout of the scale is arithmetical, like the algebraic number line, but when related to brightness one obtains ratios not differences. And these ratios are based on a logarithmic relation. For example, the apparent magnitude of the Sun makes it apparently the brightest object in the sky. But this is only because it is at 1 A.U. distance. IF “moved” to 32.6 light years (the standard candle distance to obtain absolute magnitude) then one obtains +4.8 magnitude.

So the new magnitude would be: (0.8 – 4.5) = -3.7.

That is, we locate +0.8 on the scale, then march off 4.5 units on it in direction of increased brightness.

Thus, its real magnitude -  in terms of its actual distance of 261 Ly-    makes it somewhat dimmer than it would be at the absolute magnitude distance.

The basic gist of the  magnitude scale is that every 5 increments (UNITS) in magnitude difference translates into 100 times difference in brightness, because each succeeding magnitude is different from the earlier one by 2.512 times, since:(2.515)⁵ = 100.

Thus a star of +1 magnitude is 100 times brighter than a star of +6 magnitude on the scale, since (6 – 1)= 5.

To make sure you understand the magnitude scale I attach the following problem:

Examine carefully the star magnitude positions on the given magnitude scale.

Which is brighter, Sirius or Castor, and by how many times? Which is brighter, Zosma or Sigma Draconis and by how many times? If a new star Alpha Stellaris is discovered and is found to be 15.6 times brighter than Sirius, estimate how many times brighter this new star is than Sigma Draconis.