Answer: According to author W.M. Smart ('Textbook On Spherical Astronomy', Cambridge University Press, 1931): Spherical Astronomy:
"is concerned essentially with the directions in which stars are viewed, and it is convenient to define these directions in terms of the positions on the surface of a sphere - the celestial sphere - in which straight lines joining the observer to the stars intersect the surface."
This is probably as complete a definition as one will find without going into much more details. But at the very least it's clear one requires a spherical geometry. This isn't difficult to grasp when one realizes a spherical geometry essentially was obvious from antiquity to anyone who looked up at the stars, e.g.

So what the observer would detect appeared to be on the inner surface of an immense sphere. The earliest spherical analog then was based on the central observer looking outward as if to a dome. It then was later tweaked and refined and became know as the horizon system - marked by the cardinal directions of the compass (N, S, E,W) and measuring altitude and azimuth.
The next step was for ancient observers to recognize the need for an independent spherical system with which the star positions could be pinpointed. This then introduced the celestial sphere concept:
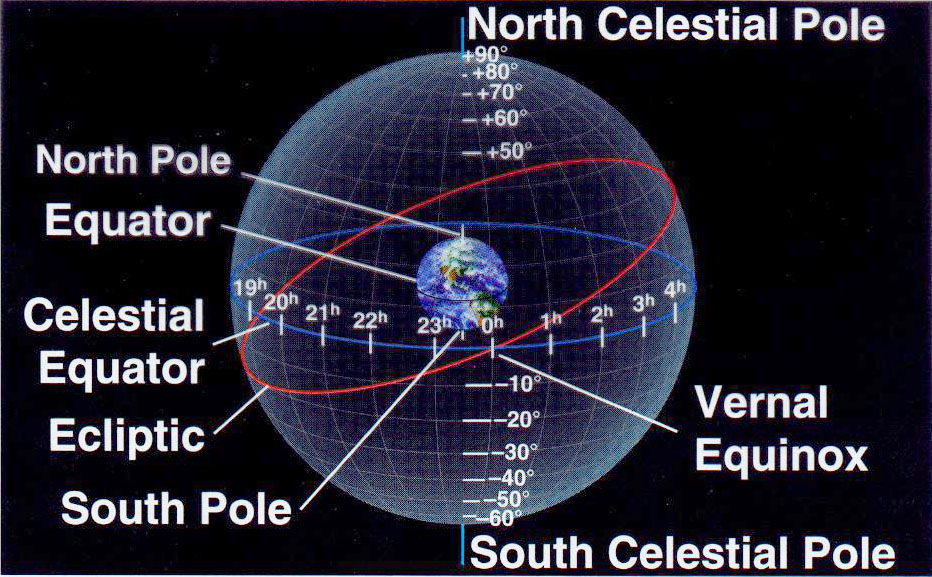
Thus, the north pole is projected to the North Celestial Pole, the equator is projected to the celestial equator, and all latitude lines are projected to become declination lines, while longitude lines become Right Ascension lines. Thus, just as every geographical location on Earth has a latitude and longitude so also every sky location has a declination and Right Ascension. The "vernal equinox" position, for example, is at 0 degrees Declination and 0 hours RA. (The vernal equinox marks the first day of spring.)
The red circle projected onto the celestial sphere defines the ecliptic or the projected (apparent) path of the Sun onto the celestial sphere through the year. If we follow the red circle - the ecliptic - UP from the vernal equinox we come to the northernmost point at +23.5 degrees declination and 6h RA. This coincides with the summer solstice - or when the Sun appears over that latitude on Earth. This marks the longest day of the year in the northern hemisphere.
So inevitably the next logical step became how to compute star positions on this sphere (which had the designated coordinates of R.A. and declination) and also how to transform between coordinate systems, say between the horizon system and the celestial sphere system.
This is critical given each such coordinate system is defined by a different set of poles and equator. For example, the coordinate system depicted in the color graphic above - the equatorial system - is based on the projections of the Earth's own equator and N. and S. poles onto the sky sphere. The poles then become the North and South Celestial poles, and the equator becomes the celestial equator. If these poles are defined respectively at +90 degrees (NCP) and -90 degrees (SCP) and the celestial equator at 0 degrees, then a system of celestial latitude can be constructed.
Once the vernal equinox position is fixed at 0 hours R.A. then the celestial longitude emerges and spans 24 hours across the same celestial sphere. (Refer again to color graphic for direction of celestial longitude circles.) These can be used in conjunction with celestial latitude (declination) to locate any celestial object. It is then possible to make computations translating one system's coordinates to those of others (horizon, ecliptic etc.)
Once the vernal equinox position is fixed at 0 hours R.A. then the celestial longitude emerges and spans 24 hours across the same celestial sphere. (Refer again to color graphic for direction of celestial longitude circles.) These can be used in conjunction with celestial latitude (declination) to locate any celestial object. It is then possible to make computations translating one system's coordinates to those of others (horizon, ecliptic etc.)
Consider
this example which seeks to find the star’s declination.
The altitude of a star as it transits your meridian is found to be 45 deg along a vertical circle at azimuth 180 deg, the south point. Find the declination d of the star.
The altitude of a star as it transits your meridian is found to be 45 deg along a vertical circle at azimuth 180 deg, the south point. Find the declination d of the star.
Since this was designed for students at latitude 13 degrees north, the key to the solution rests on the recognition that z, the zenith distance is negative. From the geometry of Fig. 3 one sees that:

90o
= z + a or z = 90o - a = 90o – 45 o = 45
o
But since we require: z = φ (latitude) = 13 o
Then z must have a negative value, or: (-45 o), since:
d = z + φ = (-45 o) + 13 o = -32 o
This makes sense, since by examining the right side of Fig. 2., the zenith distance z, plus altitude (a) must equal 90 degrees and we know CE (celestial equator) defines 0 degrees declination, then a star’s altitude of a = 45 o shows it to be SOUTH of CE. How much? Ans. 90 o - 45 o = 45 o.
But, this is still 32 o south of CE, and hence must be negative in value.
But since we require: z = φ (latitude) = 13 o
Then z must have a negative value, or: (-45 o), since:
d = z + φ = (-45 o) + 13 o = -32 o
This makes sense, since by examining the right side of Fig. 2., the zenith distance z, plus altitude (a) must equal 90 degrees and we know CE (celestial equator) defines 0 degrees declination, then a star’s altitude of a = 45 o shows it to be SOUTH of CE. How much? Ans. 90 o - 45 o = 45 o.
But, this is still 32 o south of CE, and hence must be negative in value.
Another wide application of spherical astronomy is to find the azimuth of the Sun for particular dates, and locations. In
general:
cos (A) = sin(d)/ cos (φ)
where A is the azimuth of the Sun, d denotes its declination, and φ is the observer’s latitude. (Note that d may be obtained from a table but can also be estimated from the equinox/solstice positions, i.e. +23 ½ o at solstices, 0 degrees at equinoxes.
Example: φ = 51.5 degrees N, for London
cos (A) = sin (-23.o 5)/ cos (51.o 5)
which gives approximately, 130 o.
40 degrees SOUTH of due East. (90 o + 40 o = 130 o)
Now, on the longest day of the year (say June 21), the Sun is over the Tropic of Cancer at 23.5 N latitude, so the Sun's declination is + 23. o 5 . Then the azimuth for that date is:
cos (A) = sin (23. o 5)/ cos (51. o5)
And A = 50 o
This puts the Sun's rising position North of due E. or specifically 40 degrees North of due East.
+ sin (45 o)
sin 30 o cos 60 o
We know, or can use tables or calculator to find:
cos 45 o = Ö2 / 2
cos 30 o = Ö3/ 2
sin 45 o = Ö2/ 2
sin 30 o = ½
cos 60 o = ½
Then:
cos (90 - d)= {(Ö2/ 2 )( Ö3/ 2)} + {Ö2/ 2} Ö (½) }
cos (90 - d)= Ö6/ 4 + Ö2/ 8 = {2Ö6 + Ö2}/ 8
cos (90 - d) = 0.789
arc cos (90 - d)= 37.o9
Then:
d = 90 o - 37. o 9 = 52. o 1
Or, in more technical terms:
d (star) = + 52.1 degrees

cos (A) = sin (-23.o 5)/ cos (51.o 5)
which gives approximately, 130 o.
Where
is this on our directional reference circle for azimuth? We know that 180
degrees is due South so that this must be:
40 degrees SOUTH of due East. (90 o + 40 o = 130 o)
Now, on the longest day of the year (say June 21), the Sun is over the Tropic of Cancer at 23.5 N latitude, so the Sun's declination is + 23. o 5 . Then the azimuth for that date is:
cos (A) = sin (23. o 5)/ cos (51. o5)
And A = 50 o
This puts the Sun's rising position North of due E. or specifically 40 degrees North of due East.
Now,
we can again use Fig. 3, for a celestial sphere application, in which we use the
spherical trig relations to obtain an astronomical measurement, say for declination of an object.
Using the angles shown in Fig. 3 each of the angles for the law of cosines (given above) can be found. They are as follows:
cos a = cos (90o - d)
where d = declination
cos b = cos (90 o - Lat)
Where 'Lat' denotes the latitude of the observer. Further:
Using the angles shown in Fig. 3 each of the angles for the law of cosines (given above) can be found. They are as follows:
cos a = cos (90o - d)
where d = declination
cos b = cos (90 o - Lat)
Where 'Lat' denotes the latitude of the observer. Further:
cos
c = cos z
where z here is the zenith distance.
sin b = sin (90 deg - Lat)
sin c = sin z
and finally,
cos A = cos A
Where A is the azimuth.
where z here is the zenith distance.
sin b = sin (90 deg - Lat)
sin c = sin z
and finally,
cos A = cos A
Where A is the azimuth.
Let's say we wish to find the declination of a star observed by an observer at latitude 45 o
N. The azimuth of the star is measured to be 60 o, and its zenith
distance z = 30 o. Then one would solve for cos a:
cos a = cos (90 o - d)=
cos (90 o - Lat) cos z + sin (90 o - Lat) sin z cos (A)
cos (90 o - d) = cos (90 o - 45 o) cos 30 o
cos a = cos (90 o - d)=
cos (90 o - Lat) cos z + sin (90 o - Lat) sin z cos (A)
cos (90 o - d) = cos (90 o - 45 o) cos 30 o
+ sin (90 o
- 45 o) sin 30 o cos 60 o
And:
cos (90 o - d) = cos (45 o) cos 30 o
And:
cos (90 o - d) = cos (45 o) cos 30 o
We know, or can use tables or calculator to find:
cos 45 o = Ö2 / 2
cos 30 o = Ö3/ 2
sin 45 o = Ö2/ 2
sin 30 o = ½
cos 60 o = ½
Then:
cos (90 - d)= {(Ö2/ 2 )( Ö3/ 2)} + {Ö2/ 2} Ö (½) }
cos (90 - d)= Ö6/ 4 + Ö2/ 8 = {2Ö6 + Ö2}/ 8
cos (90 - d) = 0.789
arc cos (90 - d)= 37.o9
Then:
d = 90 o - 37. o 9 = 52. o 1
Or, in more technical terms:
d (star) = + 52.1 degrees
Hopefully, this gives some small insight into the sort of computations used in spherical astronomy. As for one of the best books, you can't surpass this textbook:

When I took Spherical Astronomy & Geodesy at USF.
The problem is the book is now out of print though I suspect copies are available at university libraries. The next best option is to get hold of W. M. Smart's monograph:

When I took Spherical Astronomy & Geodesy at USF.
The problem is the book is now out of print though I suspect copies are available at university libraries. The next best option is to get hold of W. M. Smart's monograph:

Go through the text methodically, working as many problems as you can, and you will master spherical astronomy.
No comments:
Post a Comment