Spherical Astronomy Revisited (2) - Matrix Methods

In spherical astronomy one can also use matrix methods to obtain horizontal coordinates for celestial objects by using the so-called "astronmical triangle". (see image). 

The basic principle involves relating the Cartesian coordinates (rectilinear) of a point on the celestial sphere (diagram) to the curvilinear coordinates measured in the primary and secondary reference planes. One has then, for example:

(x)
(y)
(z) u,v =


(cos v .....cos u)
(cos v .....sin u)
(sin v..............)

After conversion the curvilinear coordinates may be calculated according to:

u = arctan (y/x) and v = arcsin (z)

Now, consider conventional orthogonal matrices of 3 x 3 dimensions, given as functions: R1(Θ), R2(Θ) and R3(Θ), to rotate the general system by the angle Θ about axes x, y and z, respectively. Thus we obtain:

R1(Θ) =

(1..........0................0)
(0.....cos(Θ)..... sin(Θ))
(0......-sin(Θ)....cos(Θ))


R2(Θ) =

(cos (Θ)......0........- sin(Θ))
(0................1...............0.. )
(sin(Θ)........0.......cos(Θ) )


R3(Θ) =


(cos(Θ)..........sin(Θ)..........0)
(-sin (Θ)......cos(Θ)...........0)
(0 ..................0..................1)

We now apply this method to the following generic problem:

You are located in Miami, Florida and the sidereal time = 9 h 13 m at 9.30 p.m.  local time for this date,  approximately. Saturn is visible and is at 13 h 44 m Right Ascension, and at a Declination of (- 7 ^o 56’).  If your latitude is 25. ^o75 north, find Saturn’s position  in terms of its altitude and azimuth

Solution:

We need to perform the matrix operations in the specific order:

(x)
(y)
(z) A,a = R3(-180^o) R2(90 - lat.) (XYZ(h, d)) 

Where:

R3(180) =

(cos(180)..........sin(180)..........0)
(-sin (180)...... cos(180)...........0)
(0 ..................0..................1)

Therefore: R3(-180) =

(-1       0      0)
(0       -1      0)
(0        0      1) 

And:  R2(90 ^o - lat.) =

(sin lat.       0         - cos lat.)
(0                 1                   0   )
(cos lat.      0.           sin lat.)

For which we have:

sin (lat.) = sin (25. ^o75)= 0.434 

cos (lat.) = cos (25. ^o75) = 0.900


Thence, R2(90 ^o - lat.) =

(0.434            0      -0.900 )
(0                   1               0   )
(0.900          0        0.434  )

Finally:

(x)
(y)
(z) h, d =

(cos d             cos h)
(cos d             sin h)
(sin d                 -    )

where: 

sin (d) = sin (- 7. ^o93) = -0.138

cos (d) = cos (- 7. ^o93) = 0.990

cos h = cos (-52 ^o.5) = 0.608

sin h = sin (-52 ^o.5)  =  -0.793

(Rem:  h = 9 h 13 m – 13 h 44 m =  - 3h 31m.  There are 15 degrees/ hr. 

So: -3 h 31 m » -52 ^o.5  )

Assembling the foregoing into the applicable matrix:

(0.990       0.608)
(0.990        -0.793)
(-0.138    ..........   )     =

(0.601)
(-0.785)
(-0.138)

Whence:

R3(-180 ^o) R2(90 ^o - lat.) (XYZ(h, d)) =

(-0.385)
(0.785 )
(0.481 )

The last element in the column yields the altitude, so:

a = arc sin(0.481) and a = 28. ^o  75

Meanwhile, the azimuth A =

arc tan (y/x) = arc tan (0.785/ -0.385) = -2.03

Therefore: A = arc tan(-2.03) = -63. ^o 8 

And, since its' negative, we must subtract from 360 degrees:

A= 360 ^o - 63. ^o 8   = 296. ^o 2 

Further practice problem:

Apply the  matrix method for the same location in the example problem and for the same sidereal time – but applied to the case of the planet Mars which is also visible at the same local time but at: RA = 10h 28m, and d = +12 ^o 51’.

Spherical Astronomy Revisited (1)

Spherical astronomy entails the mastery of the basic relations for spherical trigonometry. This is merely an extension of plane trig, but to the sort of angles (many > 90 degrees) one finds in astronomical applications, since distances, angles are of spherical measure (derived from spherical triangles.)        A simple illustration of spherical geometry is shown in Fig. 1. In the diagram, the angle Θ denotes the longitude measured from some defined meridian on the sphere, while the angle φ denotes a zenith distance, or the measured angle from an object to the zenith. 

Fig. 2 shows a spherical right triangle from which a host of different angle relationships can be obtained, which can then be used to find astronomical measurements, etc. 

Fig.3 shows a diagram of the celestial sphere, such as used in many practical astronomy applications, and some of the key angles with reference to a particular object (star) referenced within a given coordinate system:

In some applications, the coordinate system may not need to be changed, but in others it must - for example, when going from the coordinate system applied to sky objects (Right Ascension, Declination) to the observer's own coordinates (altitude, azimuth). In this way, coordinate transformations will also enter and are straightforward to perform, for example via use of matrices.

We consider first a simple angle relation in Fig. 1, say to find the altitude, a. Then if we have the basic geometrical relationship: a + φ = 90 degrees, then a = (90 - φ).

    Let's now examine Fig. 2 and see what spherical trig relationships we can infer.

 Two of the key ones embody the law of sines and law of cosines for spherical triangles, which are the analogs of the law of sines and cosines in plane trig.

We have for the law of sines:

Sin A/ sin a = sin B/ sin b = sin C/ sin c

where A, B, C denote ANGLES and a,b,c denote measured arcs. (Note: we could also have written these by flipping the numerators and denominators).

We have for the law of cosines:

cos a = cos b cos c + sin b sin c cos A 

Where a, b, c have the same meanings, and of course, we could write the same relationship out for any included angle.

   Now, we use Fig. 3, for a celestial sphere application, in which we use the spherical trig relations to obtain an astronomical measurement.

Using the angles shown in Fig. 3 each of the angles for the law of cosines (given above) can be found. They are as follows:

cos a = cos (90^o - d)

where d = declination

cos b = cos (90 ^o - Lat)

where 'Lat' denotes the latitude. (Recall from Fig. 1 if φ is polar distance (which can also be zenith distance) then φ = (90 - Lat))

cos c = cos z

where z here is the zenith distance.

sin b = sin (90 deg - Lat)

sin c = sin z

and finally,

cos A = cos A

Where A is the azimuth.

Example Problem:

Let's say we want to find the declination of the star if the observer's latitude is 45 ^o N, the azimuth of the star is measured to be 60 ^o, and its zenith distance z = 30 ^o. Then one would solve for cos a:

cos a = cos (90 ^o - d)=

cos (90 ^o - Lat) cos z + sin (90 ^o - Lat) sin z cos (A)

cos (90 ^o - d) =  cos (90 ^o - 45 ^o) cos 30 ^o

+ sin (90 ^o - 45 ^o) sin 30 ^o cos 60 ^o

And:

cos (90 ^o - d) = cos (45 ^o) cos 30 ^o

+ sin (45 ^o) sin 30 ^o cos 60 ^o

We know, or can use tables or calculator to find:

cos 45 ^o = Ö2 / 2

cos 30 ^o = Ö3/ 2

sin 45 ^o = Ö2/ 2

sin 30 ^o = ½

cos 60 ^o = ½

Then: 

cos (90 - d)= {(Ö2/ 2 )( Ö3/ 2)} + {Ö2/ 2} Ö (½) }

cos (90 - d)= Ö6/ 4 + Ö2/ 8 = {2Ö6 + Ö2}/ 8

cos (90 - d) = 0.789

arc cos (90 - d)= 37.^o9 

Then:

d = 90 ^o - 37. ^o 9  = 52. ^o 1

Or, in more technical terms:

d (star) = + 52.1 degrees

A more detailed image of the celestial sphere appears below with key aspects not found in the simpler version (Fig. 3):

In this detailed version we see the Earth's north pole is projected to the North Celestial Pole, the equator is projected to the celestial equator, and all latitude lines are projected to become declination lines, while longitude lines become Right Ascension lines. Thus, just as every geographical location on Earth has a latitude and longitude so also every sky location has a declination and Right Ascension.   The "vernal equinox" position, for example, is at 0 degrees Declination and 0 hours RA.  (The vernal equinox marks the  first day of spring.) 

The oblique red circle projected onto the celestial sphere defines the ecliptic or the projected (apparent) path of the Sun onto the celestial sphere through the year.  If we follow the red circle - the ecliptic - UP from the vernal equinox we come to the northernmost point at +23.5 degrees declination and 6h  RA. This coincides with the summer solstice - or when the Sun appears over that latitude on Earth. This marks the longest day of the year in the northern hemisphere

We are led then to consider how to compute star positions on this sphere (which had the designated coordinates of R.A. and declination) and also how to transform between coordinate systems, say between the horizon system and the celestial sphere  (equatorial) system.    

For example, the coordinate system depicted  in the color graphic above - the equatorial system - is based on the projections of the Earth's own equator and N. and S. poles onto the sky sphere.  The poles then become the North and South Celestial poles, and the equator becomes the celestial equator. If these poles are defined respectively at +90 degrees (NCP) and -90 degrees (SCP) and the celestial equator at 0 degrees, then a system of celestial latitude can be constructed.

 Once the vernal equinox position is fixed at 0 hours R.A. then the celestial longitude emerges and spans 24 hours across the same celestial sphere.  (Refer again to color graphic for direction of celestial longitude circles.) These can be used in conjunction with celestial latitude (declination)  to locate any celestial object. It is then possible to make computations translating one system's coordinates to those of others (horizon, ecliptic etc.) 

Example: φ = 51.5 degrees N, for London. Now, for the December (winter) Solstice the Sun is directly over the Tropic of Capricorn (φ  = 23.5 S) therefore we do know its declination is - 23.^o5. We have then for the Sun's azimuth at sunrise in London on Dec. 21:

cos (A) = sin (-23.^o 5)/ cos (51.^o 5)

which gives approximately, 130 ^o.

  Where is this on our directional reference circle for azimuth? We know that 180 degrees is due South so that this must be: 

40 degrees SOUTH of due East. (90 ^o + 40 ^o = 130 ^o)

Now, on the longest day of the year (say June 21), the Sun is over the Tropic of Cancer at 23.5 N latitude, so the Sun's declination is + 23. ^o 5 . Then the azimuth for that date is:

cos (A) = sin (23. ^o 5)/ cos (51. ^o5)

And A = 50 ^o

This puts the Sun's rising position North of due E. or specifically 40 degrees North of due East.    

Problem:

The altitude of a star as it transits your meridian is found to be 45^o along a vertical circle at azimuth 180^o, the south point.  Find the declination of the star.

Selected Questions- Answers From All Experts Astronomy Forum (Spherical Astronomy)

Question: I am a recent (2014) Mathematics graduate and would like to learn more about spherical astronomy. What exactly is it?  How does it work, i.e. what sort of computations and what objectives? And what are the best texts to get to learn more?  - Mason Dix, Louisville, KY

Answer:   According to author W.M. Smart ('Textbook On Spherical Astronomy', Cambridge University Press, 1931):  Spherical Astronomy:

"is concerned essentially with the directions in which stars are viewed, and it is convenient to define these directions in terms of the positions on the surface of a sphere - the celestial sphere - in which straight lines joining the observer to the stars intersect the surface."

This is probably as complete a definition as one will find without going into much more details. But at the very least it's clear one requires a spherical geometry.  This isn't difficult to grasp when one realizes a spherical geometry essentially was obvious from antiquity to anyone who looked up at the stars, e.g.


So what the observer would detect appeared to be on the inner surface of an immense sphere.  The earliest spherical analog then was based on the central observer looking outward as if to a dome. It then was later tweaked and refined and became know as the horizon system - marked by the cardinal directions of the compass (N, S, E,W) and measuring altitude and azimuth.

The next step was for ancient observers to recognize the need for an independent spherical system with which the star positions could be pinpointed. This then introduced the celestial sphere concept:
Thus, the north pole is projected to the North Celestial Pole, the equator is projected to the celestial equator, and all latitude lines are projected to become declination lines, while longitude lines become Right Ascension lines. Thus, just as every geographical location on Earth has a latitude and longitude so also every sky location has a declination and Right Ascension.   The "vernal equinox" position, for example, is at 0 degrees Declination and 0 hours RA.  (The vernal equinox marks the  first day of spring.) 

The red circle projected onto the celestial sphere defines the ecliptic or the projected (apparent) path of the Sun onto the celestial sphere through the year.  If we follow the red circle - the ecliptic - UP from the vernal equinox we come to the northernmost point at +23.5 degrees declination and 6h  RA. This coincides with the summer solstice - or when the Sun appears over that latitude on Earth. This marks the longest day of the year in the northern hemisphere.

So inevitably the next logical step became how to compute star positions on this sphere (which had the designated coordinates of R.A. and declination) and also how to transform between coordinate systems, say between the horizon system and the celestial sphere system.  

 This is critical given each such coordinate system is defined by a different set of poles and equator. For example, the coordinate system depicted  in the color graphic above - the equatorial system - is based on the projections of the Earth's own equator and N. and S. poles onto the sky sphere.  The poles then become the North and South Celestial poles, and the equator becomes the celestial equator. If these poles are defined respectively at +90 degrees (NCP) and -90 degrees (SCP) and the celestial equator at 0 degrees, then a system of celestial latitude can be constructed.  

Once the vernal equinox position is fixed at 0 hours R.A. then the celestial longitude emerges and spans 24 hours across the same celestial sphere.  (Refer again to color graphic for direction of celestial longitude circles.) These can be used in conjunction with celestial latitude (declination)  to locate any celestial object. It is then possible to make computations translating one system's coordinates to those of others (horizon, ecliptic etc.) 

Consider this example which seeks to find the star’s declination.

The altitude of a star as it transits your meridian is found to be 45 deg along a vertical circle at azimuth 180 deg, the south point. Find the declination  d of the star.

Since this was designed for students at latitude 13 degrees north, the key to the solution rests on the recognition that z, the zenith distance is negative. From the geometry of Fig. 3  one sees that:

90^o = z + a or z = 90^o - a = 90^o – 45 ^o = 45 ^o

But since we require: z = φ (latitude) = 13 ^o

Then z must have a negative value, or: (-45 ^o), since:

d = z + φ = (-45 ^o) + 13 ^o = -32 ^o

    This makes sense, since by examining the right side of Fig. 2.,  the zenith distance z, plus altitude (a) must equal 90 degrees and we know CE (celestial equator) defines 0 degrees declination, then a star’s altitude of a = 45 ^o shows it to be SOUTH of CE. How much? Ans. 90 ^o - 45 ^o = 45 ^o.

 But,  this is still 32 ^o south of CE, and hence must be negative in value.

Another wide application of spherical astronomy is to find the azimuth of the Sun for particular dates, and locations.  In general: 

cos (A) = sin(d)/ cos (φ)

 where A is the azimuth of the Sun,  d denotes its declination, and φ is the observer’s latitude. (Note that d may be obtained from a table but can also be estimated from the equinox/solstice positions, i.e. +23 ½ ^o at solstices, 0 degrees at equinoxes.

Example: φ = 51.5 degrees N, for London. Now, for the December (winter) Solstice the Sun is directly over the Tropic of Capricorn (φ  = 23.5 S) therefore we do know its declination is - 23.^o5. We have then for the Sun's azimuth at sunrise on Dec. 21:

cos (A) = sin (-23.^o 5)/ cos (51.^o 5)

which gives approximately, 130 ^o.

  Where is this on our directional reference circle for azimuth? We know that 180 degrees is due South so that this must be: 

40 degrees SOUTH of due East. (90 ^o + 40 ^o = 130 ^o)

Now, on the longest day of the year (say June 21), the Sun is over the Tropic of Cancer at 23.5 N latitude, so the Sun's declination is + 23. ^o 5 . Then the azimuth for that date is:

cos (A) = sin (23. ^o 5)/ cos (51. ^o5)

And A = 50 ^o

     This puts the Sun's rising position North of due E. or specifically 40 degrees North of due East.    

Now, we  can again use Fig. 3, for a celestial sphere application, in which we use the spherical trig relations to obtain an astronomical measurement, say for declination of an object.

    Using the angles shown in Fig. 3 each of the angles for the law of cosines (given above) can be found. They are as follows:

cos a = cos (90^o - d)

where d = declination

cos b = cos (90 ^o - Lat) 

Where 'Lat' denotes the latitude of the observer.  Further:

cos c = cos z

where z here is the zenith distance.

sin b = sin (90 deg - Lat)

sin c = sin z

and finally,

cos A = cos A

Where A is the azimuth. 

Let's say we wish to find the declination of a  star observed by  an observer at latitude 45 ^o N.  The azimuth of the star is measured to be 60 ^o, and its zenith distance z = 30 ^o. Then one would solve for cos a:

cos a = cos (90 ^o - d)=

cos (90 ^o - Lat) cos z + sin (90 ^o - Lat) sin z cos (A)

cos (90 ^o - d) =  cos (90 ^o - 45 ^o) cos 30 ^o

+ sin (90 ^o - 45 ^o) sin 30 ^o cos 60 ^o

And:

cos (90 ^o - d) = cos (45 ^o) cos 30 ^o

+ sin (45 ^o) sin 30 ^o cos 60 ^o

We know, or can use tables or calculator to find:

cos 45 ^o = Ö2 / 2

cos 30 ^o = Ö3/ 2

sin 45 ^o = Ö2/ 2

sin 30 ^o = ½

cos 60 ^o = ½

Then:

cos (90 - d)= {(Ö2/ 2 )( Ö3/ 2)} + {Ö2/ 2} Ö (½) }

cos (90 - d)= Ö6/ 4 + Ö2/ 8 = {2Ö6 + Ö2}/ 8

cos (90 - d) = 0.789

arc cos (90 - d)= 37.^o9 

Then:

d = 90 ^o - 37. ^o 9  = 52. ^o 1

Or, in more technical terms:

d (star) = + 52.1 degrees

Hopefully, this gives some small insight into the sort of computations used in spherical astronomy.  As for one of the best books,  you can't surpass this textbook:

When I took Spherical Astronomy & Geodesy at USF.

The problem is the book is now out of print though I suspect copies are available at university libraries. The next best option is to get hold of W. M. Smart's  monograph:

Go through the text methodically, working as many problems as you can, and you will master spherical astronomy.

Math Drives Astronomy (Pt. 2)

By the time the aspiring Astronomy major reaches his sophomore year, he will be facing even more math in courses such as Spherical Astronomy.  The emphasis here is on astronomical time (sidereal time and position - the latter based on different coordinate systems used (equatorial, horizontal, ecliptic).

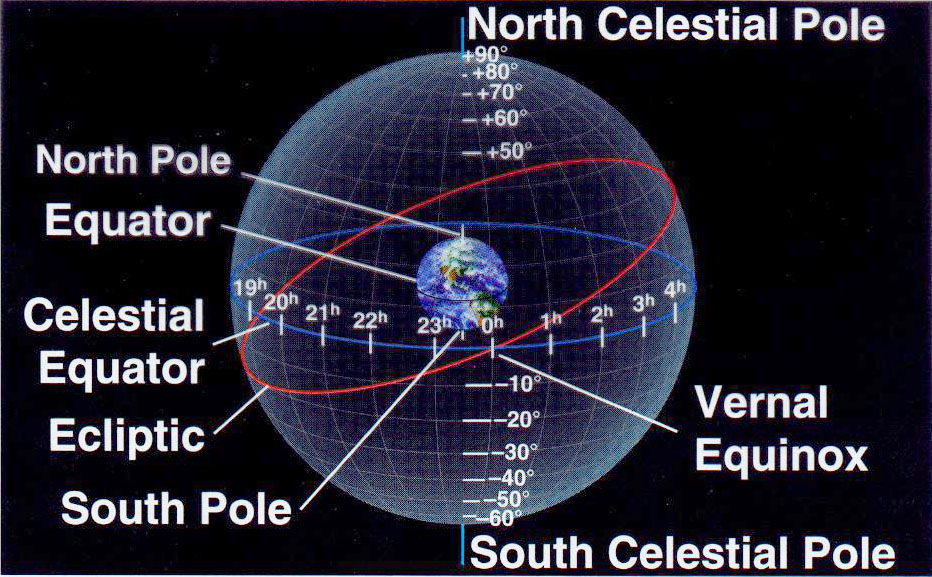
Each such coordinate system is defined by a different set of poles and equator. For example, the coordinate system depicted above - the equatorial system - is based on the projection of the Earth's N. and S. poles into the sky, as well as its equator. The poles then become the North and South Celestial poles, and the equator becomes the celestial equator. If these poles are defined respectively at +90 degrees (NCP) and -90 degrees (SCP) and the celestial equator at 0 degrees, then a consistent system of celestial latitude and longitude  can be defined in a consistent system, to locate any celestial object. We call the longitude coordinate (Θ) the Right Ascension (R.A.) while the celestial latitude coordinate is called declination and is measured in degrees north or south of the celestial equator. (In the diagram, the complementary angle of the declination is shown, φ, which we call the zenith distance.)

One of the first things the astronomy sophomore learns is how to find directions around the celestial sphere, including how to relate the R.A. to time and time keeping.  He must also do exercises showing he can find the hour angle - and distinguish it from the Right Ascension. This starts with identifying the R.A. of his local meridian (the imaginary celestial longitude passing through his zenith or highest point.)  The Right Ascension of the star is clearly equal to the local sidereal time (L.S.T.) plus the hour angle. Thus, we can write:  HA = RA of observer meridian - RA of object
Of course, before he gets very far, he will be adept at sketching any number of diagrams to solve time and position problems, such as the diagram below - with perspective looking down onto the North Celestial pole:

For example, in the diagram shown (Fig. 2) if the star's R.A. is 7h 00m and the observer is at a local sidereal time of 6h 00m, then the hour angle becomes: HA = 6h - 7h = -1h or -15 degrees. (Since every hour of longitude corresponds to 15 degrees angle, i.e. Earth turns through 15 degrees every hour, 360 degrees in 24 hours.)

The budding astronomy student will also have to know how to sketch a three dimensional diagram to enable conversion between coordinates, say from the horizontal (observer -based) to the celestial sphere. This will always include what is called the fundamental "astronomical triangle" (shaded region of Fig. 3) from which spherical trig relationships can be obtained and conversions can be made to different coordinate systems.

Using spherical trig, the student can write the law of sines and law of cosines for spherical triangles (such as shown in Fig. 3)which are analogs of the law of sines and cosines for triangles in plane trig.

We have for the law of sines:

Sin A/ sin a = sin B/ sin b = sin C/ sin c

where A, B, C denote ANGLES and a,b,c denote measured arcs. (Note: we could also have written these by flipping the numerators and denominators).

We have for the law of cosines:

cos a = cos b cos c + sin b sin c cos A

Where a, b, c have the same meanings, and of course, we could write the same relationship out for any included angle.

Now, we use Fig. 3, for a celestial sphere application, in which we use the spherical trig relations to obtain an astronomical measurement.

Using the angles shown in Fig. 3 each of the angles for the law of cosines (given above) can be found. They are as follows:

cos a = cos (90 deg - decl.)

where decl. = declination

cos b = cos (90 deg - Lat)

where 'Lat' denotes the latitude. (Recall from Fig. 1 if φ is polar distance (which can also be zenith distance) then φ = (90 - Lat))

cos c = cos z

where z here is the zenith distance.

sin b = sin (90 deg - Lat)

sin c = sin z

and finally,

cos A = cos A

where A is azimuth.

Let's say we want to find the declination of the star if the observer's latitude is 45 degrees N, and the azimuth of the star is measured to be 60 degrees, with its zenith distance z = 30 degrees. Then one would solve for cos a:

cos a = cos (90 deg - decl.)=

cos (90 deg - Lat) cos z + sin (90 deg - Lat) sin z cos (A)

cos (90 deg - decl.) =

 

cos (90 - 45) cos 30 + sin (90 - 45) sin 30 cos 60

 

And:

cos (90 deg - decl.)= cos (45) cos 30 + sin (45) sin 30 cos 60

We know, or can use tables or calculator to find:

cos 45 = [2]^½/ 2

cos 30 = [3]^½/ 2

sin 45 = [2]^½/ 2

sin 30 = ½

cos 60 = ½

Then:

cos (90 deg - decl.)= {([2]^½/ 2 )([3]^½/ 2)} + {[2]^½/ 2} (½) (½)

cos (90 deg - decl.)= [6]^½/ 4 + [2]^½/ 8

 

= {2[6]^½ + [2]^½}/ 8

cos (90 deg - decl.)= 0.789

arc cos (90 deg - decl.)= 37.9 deg

Then:

decl. = 90 deg - 37.9 deg = 52.1 deg

Or,  decl. (star) = + 52.1 degrees

 

The student will also become familiar with matrix methods for converting between the different coordinate systems.

 

The basic principle involves relating the Cartesian coordinates (rectilinear) of a point on the celestial sphere (diagram) to the curvilinear coordinates measured in the primary and secondary reference planes. One has then, for example:

(x)
(y)
(z) u,v =


(cos v .....cos u)
(cos v .....sin u)
(sin v..............)

After conversion the curvilinear coordinates may be calculated according to:

u = arctan (y/x) and v = arcsin (z)

Now, consider conventional orthogonal matrices of 3 x 3 dimensions, given as functions: R1(Θ), R2(Θ) and R3(Θ), to rotate the general system by the angle Θ about axes x, y and z, respectively. Thus we obtain:

R1(Θ) =

(1..........0................0)
(0.....cos(Θ)..... sin(Θ))
(0......-sin(Θ)....cos(Θ))


R2(Θ) =

(cos (Θ)......0........- sin(Θ))
(0................1...............0.. )
(sin(Θ)........0.......cos(Θ) )


R3(Θ) =


(cos(Θ)..........sin(Θ)..........0)
(-sin (Θ)......cos(Θ)...........0)
(0 ..................0..................1)


To fix ideas, say you wish to obtain the horizontal coordinates (A, a) for some object in the sky and you know its R.A. and decl. from an almanac.  Then the procedure is fairly straightforward, and entails writing:

 

R3(Θ) = R3(-180 deg)

R2(Θ) = R2(90 - lat.)

so that:

(x)
(y)
(z) A,a = R3(-180 deg) R2(90 - lat.) (XYZ(h, decl.))

 

where : (XYZ(h, decl.)) =

(x)
(y)
(z) h,decl.

 

Bear in mind: R3(-180 deg) =

(cos 180........-sin 180................0)
(sin 180........cos 180................0)
(0......................0......................1)

And:R3(Θ) =


(cos(Θ)..........sin(Θ)..........0)
(-sin (Θ)......cos(Θ)...........0)
(0 ..................0..................1)

Therefore: R3(-180) =

(-1.....0.......0)
(0.......-1.....0)
(0.......0.......1)

Obtaining R2(Θ) = R2(90 - lat.) is just as easy, if one recalls the basic trig identity:

cos (90 - φ) = sin (φ)

 

Not surprisingly, it is the sophomore year at which point most wannabe Astronomy majors change their minds and either drop out entirely or change their major - say to a less mathematically demanding subject. At the Univ. of South Florida, nearly 60% had dropped out by the end of the quarter which featured spherical astronomy.