Products of Two Vectors:
Dot Product:
In the diagram below we show the geometry relevant to the scalar
product of two vectors, say A ·B.
The scalar product of two vectors A and B is also called the dot product because of the dot symbol used to denote it. Thus:
A ·B = ‖A‖ ‖B‖ cos Θ, hence also:
cos(Θ)
= (A ·B)/
[A][B]
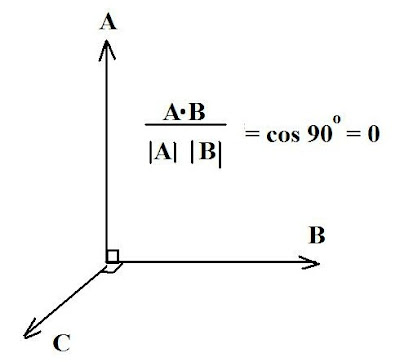
If the two vectors are at a right angle to
each other then Θ = 90 degrees and:
cos(Θ) = (A ·B)/
[A][B] = 0
Since vector multiplication is commutative, we
also have:
A ·B = B ·A
Vector Cross Product:
The
vector cross product A X B is illustrated below:

Here, we let the angle subtended between A and B be Θ with: 0 < Θ < π. Then unless A and B are parallel, they now determine a plane. Let n be a unit vector perpendicular to the plane and pointing in the direction a right-handed thread screw would advance when its head is rotated from A to B through the angle Θ. The vector product or cross product is then:
A X B = n ‖A‖ ‖B‖ sin Θ
It
is clear that if A and B are parallel (Θ = 0) so:
A X B =
0
Also,
if A
and B are reversed in the depiction
above, then it follows the unit vector n
is replaced by – n and hence:
B X A = - A X B
A = a x i + a y j + a z k
B = b x i + b y j + b z k
Then the cross product can be conveniently written as a 3rd order determinant:
A X B = [ i j k ]
[ a x a y a z ]
[ b x b y b z]
Triple Scalar Product:
We refer to the product: (A X B)
· C as the triple scalar product,
given that it is derived from vector dimensions in a solid geometry
setting. On inspection of the diagram
below, of a paralleilepiped, we see the vector N = A X B
is normal to the base (determined by the vectors A, B) so equals to the
area of that base. Thus:
(A X B) · C = ‖N‖ ‖C‖ cos Θ
Thus: N
= A X B= area of the base
And: ‖C‖ cos Θ = +
altitude of the box
Given A is defined: A = a 1 i + a 2 j + a 3 k
And:
B = b 1 i + b 2 j + b 3 k
And C similarly, with:
(A X B) · C = A · B X C
The
triple scalar product can be expressed:
(A X B) · C
= [a 1 a 2 a 3
]
[ b 1 b 2 b 3]
[ c 1
c 2
c 3]
Triple Vector Product:
Represent the product of three vectors A, B
and C with two equations that are companions of each other:
(A X B) X C =
(A · C ) B
- (B · C ) A
And:
A X (B X C) = (A
· C ) B
- (A · B ) C
Example Problem: Show the two identities are equal by computing:
A X (B X C) two different ways, if:
A X (B X C) two different ways, if:
A = i – j + 2k
B = 2i + j + k
C = i + 2j - k
Solution:
We first use:
(A X B) X C =
(A · C ) B
- (B · C ) A
Whence:
A · C =
-3 And B · C =
3
And:
(A · C )
B -
(B · C )
A = -3B - 3 A
(A · C )
B -
(B · C )
A = -3B - 3 A
= -3 (2i + j + k) -
3(i – j + 2k ) = -6i – 3i – 3k – 6k
= - 9i - 9 k
Using
the method of determinants:
A X B = [ i j
k ]
[ a x a y a z]
[ b x b y
b z]
So:
A X B = [ i j
k ]
[ 1 -1 2]
[ 2 1 1 ]
= – 3i + 3j + 3 k
But:
(A X B) X C
= [ i j
k ]
[ -3 3 3 ]
[ 1 2 -1]
= - 9i - 9 k
Problems:
1) For a vector A = 3i
– 2j – k find the magnitude of the vector product: A X
A.
2) A cube has edges of
length 2a, with center at 0 and its sides are parallel to the coordinate planes
of an xyz coordinate system. What are
the position vectors of the corners?
3) Find A X B if A = 2i - 2j -k, and B = i + j + k.
4) Find a vector perpendicular to both of the vectors A = i + j + k and B = i + j
5) Let A = i + j, B = 2i - 3j -k and: C = 4j - 3k
Show that: (A X B) X C = A X (B X C)
Using the determinant method.
3) Find A X B if A = 2i - 2j -k, and B = i + j + k.
4) Find a vector perpendicular to both of the vectors A = i + j + k and B = i + j
5) Let A = i + j, B = 2i - 3j -k and: C = 4j - 3k
Show that: (A X B) X C = A X (B X C)
Using the determinant method.

No comments:
Post a Comment