
Cepheid Variables and the Period-Luminosity Law
With this blog, we'll being looking at intermediate level astronomy problems, and start with the Period-Luminosity law for Cepheid Variables. Cepheids are variable stars named after the prototype, Delta Cephei. Type I Cepheids (classical), typically have periods from 2 – 100 days, and a range of median absolute magnitudes from (-1.5) to (-5). Characteristically, they are supergiants of spectral class F to G, The reason for brightness fluctuations can be attributed to regular pulsations of the star.
The use of Cepheids is particularly crucial in obtaining astronomical distances since the method of trigonometric parallaxes breaks down at a distance of about 50 pc (163 LY). The reason is that by this time the parallx angle p becomes much too small to measure accurately. Hence, astronomers look to the Cepheids, the "headlamps of the heavens" to provide a distance gauge.
Like all variable stars, the Cepheids undergo periodic fluctuations in their apparent brightness. However, their use as distant indicators is based on a specific relationship between their periods and their intrinsic brightness or luminosity. This "Period-Luminosity Law" was discovered by Ms. Henrietta Leavitt in 1912. Basically, the law states that the longer the period of a given Cepheid, the greater the intrinsic brightness.
The operative principle is that if we know the intrinsic brightness (e.g. read off from the attached graph on the vertical axis, then we know the period in days). Then the distance to the star can be foujnd by using the inverse square law of light propagation. I.e.
(d1/d2)^2 = B2/ B1
where d1 and d2 are the distances of two objects, and B1, B2 their respective brightnesses. See also my earlier blog on brightness and the stellar magnitude scale:
http://brane-space.blogspot.com/2011/07/tackling-simple-astronomy-problems-3.html
Thus, if we observe two Cepheids with equal periods, say P1 = P2, and one appears to be one-fourth as bright as the other, i.e. B2 = ¼ B1, we can infer on the basis of the inverse square law for light that the apparently dimmer one is twice the distance of the apparently brighter one (e.g. d2 = 2d1).
It's of interest to note here that the relative error associated with Cepheid distance determinations is completely independent of the distance. This contrasts markedly with the situation for the trigonometic parallax for which the error increases with increasing distance.
Classical Cepheids in neighboring galaxies can also be used to find distances. The procedure entails first identifying the Cepheids within the other galaxies and determining their periods. Again, the P-L relationship is utilized. (But for very distant galaxies even the Cepheid method breaks down).
Example Problem:
ON the graph showing the Period-Luminosity law, two Cepheids are shown, A and B.
a) Compare the periods of the two stars, in days.
b) How much brighter is the longer period star than the other.
Solution.
a) The periods can be read off along the horizontal axis. For Cepheid A we have Log P = 1.2, so P = 15.8 days (e.g. antilog(base 10) of 1.2 = 15.8). Similarly, for Cepheid B we have Log P = 0.65 (est.) so P = 4.4 days.
b) The longer period Cepheid (A) is 2.512 times brighter than the shorter period one, B, since there is 1 magnitude difference,
M_v(A) - M_v(B) = [(-4) - (-3)] = -1
and each magnitude is different from one that's a unit brighter, by 2.512 times, since: (2.515)^5 = 100.
Other Problems:
1) For the example problem given, if the distance to Cepheid A = 10 pc, find the distance to Cepheid B.
2) One Cepheid is found to have a period of 6.32 days and a mean apparent magnitude of +4.5. Another Cepheid in the same constellation is found to have a period of 15.9 days and a mean apparent magnitude of +7. If the P-L relationship for both has an uncertainty of +/- 0.35 m, find the approximate distance for each one.
3) Two Cepheids, Alpha and Beta are observed to have the same period of 10 days. at maximum brightness A has an apparent magnitude of +3.0 and B has an apparent magnitude of +8.0. If the distance of A (associated with a cluster) is known to be 60 pc, how far away is B?
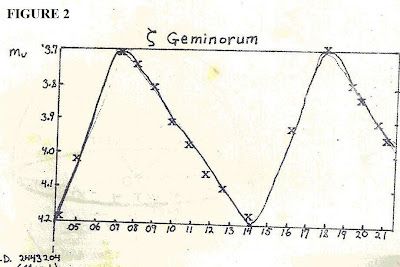
4) A CXC astronomy student plots a light curve for the Cepheid Zeta Geminorum as shown (Fig. 2). Using this curve and the P-L graph, estimate the brightness of this Cepheid in terms of absolute visual magnitude.
No comments:
Post a Comment