Answer: The celestial sphere, probably since antiquity, has been perceived as a sphere of infinite radius, only half of which we can see at any one time. (The other half on the opposite side of Earth). Using it to fix on the distant stars, it also appears to be rotating in an east-west direction. Basically, it is a result of projecting the Earth's own latitude and longitude lines - as well as the Earth's north and south poles - onto the sky, thereby yielding a corresponding sphere in the sky which has its own coordinate system. This can then be used to locate sky objects presumed to be on its interior surface.
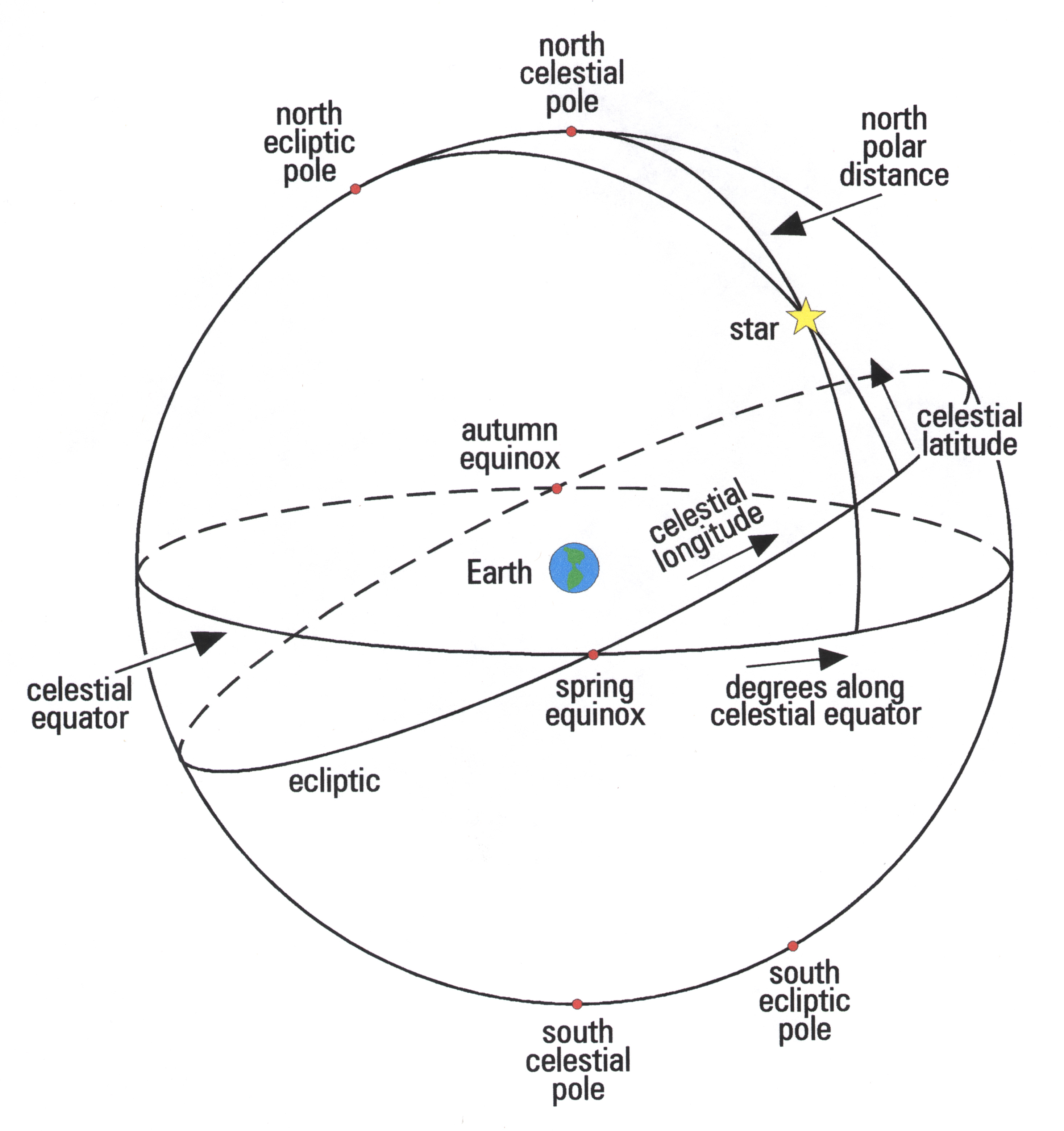
The projected coordinates corresponding to latitude circles are called declination, and those corresponding to longitude are called Right Ascension. Given this, the "celestial equator" would simply be the Earth's own equator (latitude 0 degrees) projected onto the sky sphere, while the North Celestial Pole is the projection of the Earth's north pole and the South Celestial Pole is the projection of the south pole. These projections are shown on the accompanying diagram.
In effect, the "design" of the celestial sphere is such that if one were travel to one of the Earth's geographical poles, the corresponding celestial pole would be directly overhead (at the zenith). If one were to travel to Earth's equator, the celestial equator would pass directly through your zenith.
Declination circles, like latitude circles, run in the east-west direction parallel to the celestial equator, starting at 0 degrees and increasing to +90 degrees (North celestial pole or NCP). Also decreasing in the opposite direction to (-90) degrees, or the South celestial pole. When one superimposes these lines one would envisage this more complete celestial coordinate system:
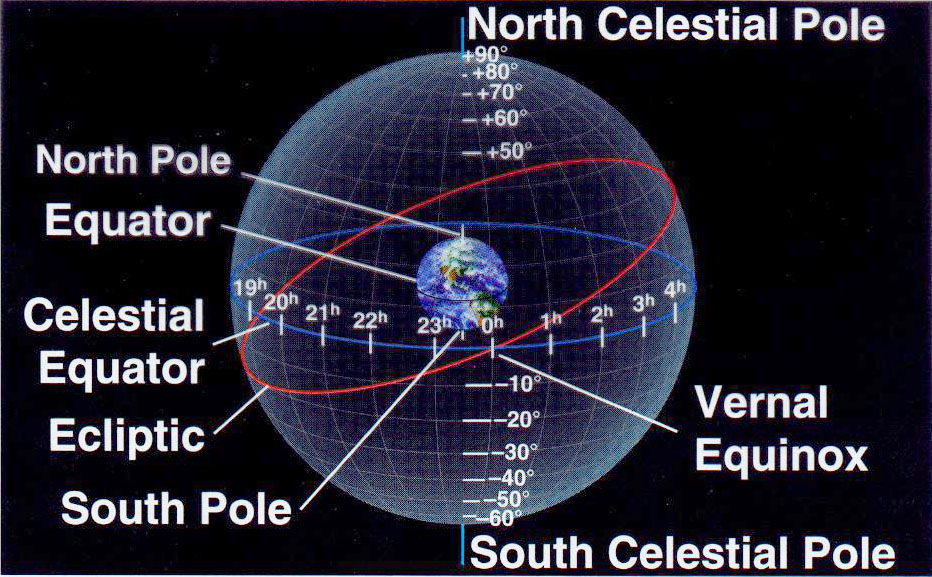
The other celestial sphere coordinate, Right Ascension, corresponds to Earth longitude. Both longitude and Right Ascension circles run from pole to pole. However, the 'prime meridians' are different. For Earth, the prime meridian of longitude is the same as the Greenwich meridian defined as 0 degrees. All longitude circles to the west, e.g. Barbados at 60 degrees W., are designated such that times are earlier than a calibrated clock reads at Greenwich. All longitude circles to the east are designated as having later times than at Greenwich.
By contrast, for Right Ascension we need to use a specific abstract point in the sky, called the Vernal Equinox, to mark the meridian of origin. This is the point at which the Sun - on its journey north (seen as a projection via the ecliptic on the celestial sphere) crosses the celestial equator. This is visible in the second diagram, where you will see the reddish line for the ecliptic (which is the projection of the Sun's apparent path onto the celestial sphere). Bear in mind here, the Sun is not really moving across the sky. It is only the appearance of such because the Earth is really doing the moving, i.e. orbiting about the Sun. Hence, in a real sense, the ecliptic is the projection of Earth's own orbital motion onto the celestial sphere, but which is embodied in the Sun's apparent path.
The point called the Vernal Equinox - as can be seen in the diagram - occurs on or about March 21 each year. Now, the celestial circle of longitude which passes through the Vernal Equinox is defined as 0 hours Right Ascension. Note here that Right Ascension is measured in hours and minutes (60 minutes being equal to one hour), and increases numerically eastwards from the Vernal Equinox This would be continuously (unlike Earth longitude - which divides into E. and W. ) from 0h through 24 h.
Using the design conventions given here any astronomical object, planet, star, star cluster, etc. can be pinpointed by coordinates in the night sky.
No comments:
Post a Comment