
Telescopic image of the type that might normally be visible at opposition.
The good news for astronomy buffs and sky observers? The Red Planet Mars is at its closest distance in 15 years - barely 35.8 million miles from Earth this evening. The bad news? The planet is currently in the throes of a massive dust storm - obscuring details (see image) normally visible through Earth bound telescopes. (The Martian atmosphere is currently so inundated by dust that NASA's Opportunity Rover hasn't been able to recharge. There simply isn't enough sunlight to get through to its solar panels.)
For reference, Mars came to the configuration known as opposition on July 27th or 4 days ago. That meant that Mars and the Sun were on exactly opposite sides of Earth, conforming to the dotted alignment S-E-p shown below
.

Two relevant questions are:
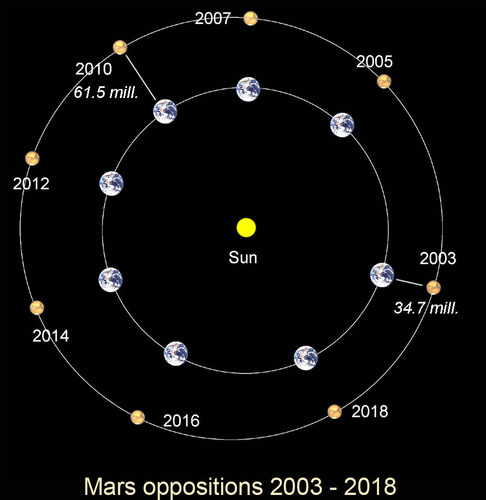
1) Why don't Martian oppositions occur at the same distances relative to Earth each time? (See e.g. the color graphic showing different Mars-Earth distances for Mars' oppositions over 2003-18)
and
2) Why do the dates of opposition and closest approach usually differ?
In respect to (1) the reason is basically to do with Mars having a more elliptical orbit (eccentricity e = 0.093) than Earth. All planets have elliptical orbits featuring a perihelion (closest point to Sun) and aphelion (farthest point) On account of Mars' orbit being more elliptical, Mars perihelion distance from the Sun can vary by about 26 million miles. By contrast, Earth's perihelion distance - because of its more circular orbit - doesn't vary by more than 3 million miles. As you can see, our planet's perihelion variation and Mars perihelion variation are dramatically different. But it is this variation that accounts for the differing distances at Martian oppositions (see color graphic) Near - or distant - oppositions of Mars recur every 15-17 years.
In respect of (2) we note Earth being closer to the Sun than Mars means it takes less time to make its circuit than the Red Planet. (365.25 days vs. 687 days). In addition, Earth's perihelion arrives yearly in January, while Mars arrives on Sept. 16. At the alignment SEp shown in the diagram (p for Mars), for the date July 27 - when Earth was directly between Mars and the Sun - Mars was still drawing closer to the Sun (remember its perihelion date is Sept. 16). Because of this disparity the closest distance between the two worlds occurs tonight, as opposed to 4 days ago. For those curious about the length of the disparity, the time can be as long as 8.5 days (in 1969) or as brief as 10 minutes (in 2208 and 2232).
Critical to determining these variations is measuring the synodic period of Mars. In general, we define the synodic period to be the time interval for the revolution of a planet as determined from the same phase, or the same geometrical configuration. In this case between successive Martian oppositions.
Now, over t days, the 180 degree 'straight' angle, i.e. at opposition, will have increased to a value Θ given by the angle SE1 p1 or :
Θ = [n - n(p)] t
where n, n(p) are the mean daily motions of the Earth and the planet, (Mars) respectively, and t is in days. Using the respective sidereal periods for Earth (P) and Mars ( P') we may write:
n = 0.98564 deg/day = 360/P where P = 365.25 days
n(p) = n(Mars) = 0.52407 deg /day = 360/P' where P' = 687 days
Then:
Θ = 360 (1/P - 1/P') t
The synodic period (S) of the planet (Mars) is then found (with t = 1 day):
Θ = 360 (1/S) = 0.462 deg
Or: S = 360 deg/day / Θ deg = 360 /0.462 = 780 days
The synodic period can also be found in more direct form, viz.
1/S = 1/P - 1/P'
1/ S = 1/ 365.25 - 1/ 687 = 0.001282
So: S = 1/ 0.001282 = 780 days
Knowing the period S allows one to answer the question 'How long until Earth and Mars are lined up, i.e. at opposition, again?' So the inner planet (e.g. E, Earth in this case) will make one circuit around the Sun then catch up to the outer one (Mars or P in the diagram) to reform the alignment. Thus, Earth laps the outer planet (Mars) so as seen from the Earth the synodic period will be longer than the sidereal one (measured with reference to the stars). The inner planet (Earth) moves at 360/ P degrees per day, while the outer planet (Mars) moves at the slower rate of 360/ P' per day. So at the end of one day Earth will have gained an angle of (360/P - 360/ P') degrees. This puts the answers to (1) and (2) above in context.
Another reason for viewing Mars tonight - despite the dust storm conditions on its surface - is the recent announcement that an advanced radar satellite (MARSIS) has detected subglacial liquid water. An Italian research team (Roberto Orosei et al) found what appears to be a massive 12 mile long lake that is believed to be at least a meter deep. The Italian team published their work in the journal Science last Wednesday and readers can read more about it here:
Comprehension Question:
Show algebraically how to go from the equation: Θ = 360 (1/P - 1/P') t
To the basic (more direct) form: 1/S = 1/P - 1/P'
Justify from a physical perspective why the equations are really the same.
No comments:
Post a Comment