In the previous instalment we saw how the simple stellar properties of mass and luminosity (intrinsic brightness) can be obtained. Now, we will extend that to see how a star's radius and effective temperature can be found. Once again, all of these properties have been enabled by work on binary stars - which allows mass and luminosity (for main sequence or stable stars) and then further basic extrapolations from these.
Stellar mass and radius essentially come about by relating the star's luminosity (L') to its surface area (A = 4π R^2) and simultaneously to its total energy output (E = sT'_eff^4), where T'_eff is the surface or effective stellar temperature, and s is the Stefan -Bolztmann constant. When the two are combined, the stellar luminosity can be expressed as:
L' = 4π R'^2 (sT_eff^4)
Or in simple logarithmic form (in terms of the solar values L, T, and R):
Log (L'/L) = 4 Log (T'_eff/T_eff) + 2 Log (R'/R)
Where T_eff = 5760 K or the Sun's effective (surface) temperature.
Example Problem:
If the star Sirius A has a mass of approximately twice the Sun's and an effective temperature of 10 000 K, find its radius in terms of the Sun's and also the actual value if the Sun's is R = 6.9 x 10^5 km.
Solution:
Using the mass luminosity law from before, then if (M'/M) = 2:
Log (L'/L) = 3.5 Log (2) = 3.5 (0.301) = 1.053
And:
Log (L'/L) = 1.053 = 4 Log (T'_eff/T_eff) + 2 Log (R'/R)
Or, for radius:
2 Log (R'/R) = 1.053 - 4 [Log(T'_eff/ LogT_eff)]
Whence:
2 Log (R'/R) = 1.053 - 4 (Log 10000 - Log 5760)= 1.053 - 4(4.00 - 3.76)
2 Log (R'/R) = 1.053 - 0.960 = 0.930
Log (R'/R) = (0.930)/2 = 0.0465
and taking antilogs:
R'/R = 1.11 or R' = 1.11 R
So Sirius A's radius is about 1.1 times the Sun's
Or:
R' = 1.1 (6.9 x 10^5 km) = 7.6 x 10^5 km
It's well to add a cautionary note here that the radius worked out using the preceding nethod is not the same as that derived from the absolute bolometric magnitude of Sirius.
To show this, note the absolute visual magnitude of Sirius is +1.4 and the bolometric correction corresponding to it is (-0.56). Then the absolute bolometric magnitude is:
M_bol* = M_V + B.C. = +1.4 + (-0.56) = +0.84
The luminosity in terms of the Sun's is then:
Log (L'/L) = 0.4 (M_bol - M_bol*)
Log (L'/L) = 0.4 (4.63 - 0.84) = 1.516
And:
2 Log (R'/R) = 1.516 - 0.960 = 0.556
So:
Log (R'/R) = 0.556/2 = 0.278
Antilog (0.278) = 1.9 (approx.)
Or: R' = 1.9 R
Or, 1.9 times the solar radius.
Which is correct? In fact, both values have uncertainties but the latter value is at least closer to the actual radius, based as it is on more accurate photometric measurements. Besides, the mass-luminosity law (as we saw) is an empirical relationship and also varies over the main sequence (e.g. depending on temperature and luminosity) so we can expect it to differ when used for stars on the upper main sequence, compared to the lower. These refinements, of course, are taken into account in advanced astrophysics- astronomy, but since we are working at an intermediate level, we don't do so here.
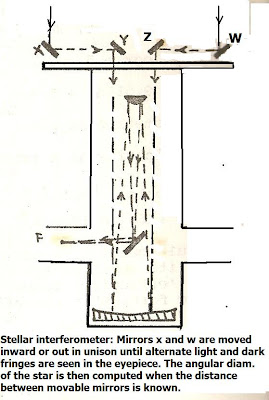
Observationally, one method of measuring a star's radius is by using an interferometer such as shown in the sketch. This employs the principle of interference to obtain an angular measurment for the star's apparent diameter (e.g. in arcsec or "). If the distance to the star is known then one can get the radius of the star R* in terms of the Sun's R, by using:
R*/R = (d* a*")/ (d a")
In the foregoing, a" denotes the apparent angular diamter of the sun (1920"), d is the Sun's distance (1 AU = 1.495 x 10^8 km), d* is the star's distance and a*" is the star's apparent angular diameter.
Example Problem:
Find the radius of the star Regulus if its distance is 24 pc and its apparent angular diameter from interferometer measurements is 0."0018.
Solution:
First convert the star's distance to AU to be able to conform with d (= 1 AU)
We know that 200,000 AU = 1 pc, then:
24 pc x (2 x 10^5 AU/pc) = 48 x 10^5 AU
Then:
R*/R = (4.8 x 10^6) x (0."0018/ 1920") = (8640/1920) = 4.5
So: R* = 4.5 R
So Regular has a radius 4½ times that of the Sun.
Other problems:
1) Find the radius of the star Alhena from Problem (1) in the previous problem set. (Use the same data available)
2) Use two different techniques to arrive at the radius of the star Beta Pegasi, which lies at a distance of 50 pc and has: (B - V) = +1.7 and m_v = 2.5. Interferometry obtains the apparent angular diameter as 0."021.
a) What is the apparent discrepancy (as a percentage) in the two values obtained?
b) Account for these discrepancies.
c) Which value, if any, would you be inclined to assign as having greater accuracy?
3) Consider the stars below and their (B- V) and M_V values:
Rigil Kent : (B - V) = 0.71, M_V = 4.2
Spica: (B - V) = -0.23, and M_V = (-3.1)
Fomalhaut: (B - V) = 0.09 and M_V = 1.9
Suhail: (B - V) = 1.7 and M_V = (-4.3)
a) Find the mass, luminosity and radius of each of these stars.
b) Try to estimate the surface temperature of each of these stars. (Hint: you can use the data from the Table of Bolometric corrections in the previous instalment).
Stellar mass and radius essentially come about by relating the star's luminosity (L') to its surface area (A = 4π R^2) and simultaneously to its total energy output (E = sT'_eff^4), where T'_eff is the surface or effective stellar temperature, and s is the Stefan -Bolztmann constant. When the two are combined, the stellar luminosity can be expressed as:
L' = 4π R'^2 (sT_eff^4)
Or in simple logarithmic form (in terms of the solar values L, T, and R):
Log (L'/L) = 4 Log (T'_eff/T_eff) + 2 Log (R'/R)
Where T_eff = 5760 K or the Sun's effective (surface) temperature.
Example Problem:
If the star Sirius A has a mass of approximately twice the Sun's and an effective temperature of 10 000 K, find its radius in terms of the Sun's and also the actual value if the Sun's is R = 6.9 x 10^5 km.
Solution:
Using the mass luminosity law from before, then if (M'/M) = 2:
Log (L'/L) = 3.5 Log (2) = 3.5 (0.301) = 1.053
And:
Log (L'/L) = 1.053 = 4 Log (T'_eff/T_eff) + 2 Log (R'/R)
Or, for radius:
2 Log (R'/R) = 1.053 - 4 [Log(T'_eff/ LogT_eff)]
Whence:
2 Log (R'/R) = 1.053 - 4 (Log 10000 - Log 5760)= 1.053 - 4(4.00 - 3.76)
2 Log (R'/R) = 1.053 - 0.960 = 0.930
Log (R'/R) = (0.930)/2 = 0.0465
and taking antilogs:
R'/R = 1.11 or R' = 1.11 R
So Sirius A's radius is about 1.1 times the Sun's
Or:
R' = 1.1 (6.9 x 10^5 km) = 7.6 x 10^5 km
It's well to add a cautionary note here that the radius worked out using the preceding nethod is not the same as that derived from the absolute bolometric magnitude of Sirius.
To show this, note the absolute visual magnitude of Sirius is +1.4 and the bolometric correction corresponding to it is (-0.56). Then the absolute bolometric magnitude is:
M_bol* = M_V + B.C. = +1.4 + (-0.56) = +0.84
The luminosity in terms of the Sun's is then:
Log (L'/L) = 0.4 (M_bol - M_bol*)
Log (L'/L) = 0.4 (4.63 - 0.84) = 1.516
And:
2 Log (R'/R) = 1.516 - 0.960 = 0.556
So:
Log (R'/R) = 0.556/2 = 0.278
Antilog (0.278) = 1.9 (approx.)
Or: R' = 1.9 R
Or, 1.9 times the solar radius.
Which is correct? In fact, both values have uncertainties but the latter value is at least closer to the actual radius, based as it is on more accurate photometric measurements. Besides, the mass-luminosity law (as we saw) is an empirical relationship and also varies over the main sequence (e.g. depending on temperature and luminosity) so we can expect it to differ when used for stars on the upper main sequence, compared to the lower. These refinements, of course, are taken into account in advanced astrophysics- astronomy, but since we are working at an intermediate level, we don't do so here.
Observationally, one method of measuring a star's radius is by using an interferometer such as shown in the sketch. This employs the principle of interference to obtain an angular measurment for the star's apparent diameter (e.g. in arcsec or "). If the distance to the star is known then one can get the radius of the star R* in terms of the Sun's R, by using:
R*/R = (d* a*")/ (d a")
In the foregoing, a" denotes the apparent angular diamter of the sun (1920"), d is the Sun's distance (1 AU = 1.495 x 10^8 km), d* is the star's distance and a*" is the star's apparent angular diameter.
Example Problem:
Find the radius of the star Regulus if its distance is 24 pc and its apparent angular diameter from interferometer measurements is 0."0018.
Solution:
First convert the star's distance to AU to be able to conform with d (= 1 AU)
We know that 200,000 AU = 1 pc, then:
24 pc x (2 x 10^5 AU/pc) = 48 x 10^5 AU
Then:
R*/R = (4.8 x 10^6) x (0."0018/ 1920") = (8640/1920) = 4.5
So: R* = 4.5 R
So Regular has a radius 4½ times that of the Sun.
Other problems:
1) Find the radius of the star Alhena from Problem (1) in the previous problem set. (Use the same data available)
2) Use two different techniques to arrive at the radius of the star Beta Pegasi, which lies at a distance of 50 pc and has: (B - V) = +1.7 and m_v = 2.5. Interferometry obtains the apparent angular diameter as 0."021.
a) What is the apparent discrepancy (as a percentage) in the two values obtained?
b) Account for these discrepancies.
c) Which value, if any, would you be inclined to assign as having greater accuracy?
3) Consider the stars below and their (B- V) and M_V values:
Rigil Kent : (B - V) = 0.71, M_V = 4.2
Spica: (B - V) = -0.23, and M_V = (-3.1)
Fomalhaut: (B - V) = 0.09 and M_V = 1.9
Suhail: (B - V) = 1.7 and M_V = (-4.3)
a) Find the mass, luminosity and radius of each of these stars.
b) Try to estimate the surface temperature of each of these stars. (Hint: you can use the data from the Table of Bolometric corrections in the previous instalment).
No comments:
Post a Comment