Algebraic homology is a branch of topology that is used to analyze higher-dimensional structures. This is accomplished by first converting them into flat, two-dimensional configurations, then assigning algebraic symbols to each 'dimension' (chain). Let's consider a relatively simple example: the basic torus pattern shown below:
Thus, for the ‘top’ side of the torus:
A ---->-----D ----->------ A
and, for the ‘bottom’ side:
One could go one step further, as I indicated, and assign Greek letters to the different segments. For example:
a : A ---->-----D -----> ------ A
b : A ---->-----D -----> ------ A
We now have a one-dimensional homology space (H1) denoted by:
H1 = ( a + b )
The same applies to the complementary homology space (H1') that runs vertically so as to join the left and right sides, which we might denote by:
H1' = (d + g)
1 –Simplex:
A 1-simplex can be represented as follows:
a1 ---->-----a: -----> ------ a2
Then the boundary of a 1-simplex is given by:
¶ 1 a = ¶ 1
(a1 a2) = a2 - a1
¶ 0 (a1) = 0 which defines a “node”.
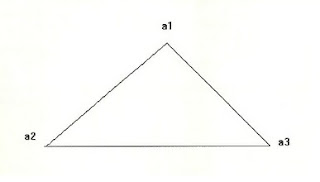
2 –Simplex:
Likewise the boundary of a
2-simplex, e.g.
Is defined by: ¶ 2 (a1 a2 a3 ) = a2 a3 – a1 a3 + a1 a2
But the 2-simplex is ordinarily depicted
with greater generality as:
So that, the sum of k-chains, for a complex C 2 can be expressed :
C 2 = åk x i 2 i = 1
Where x i 2 denotes a directed line segment, e.g. a2 a3 and the superscript denotes the dimension. So the applicable boundary operator is specified:
¶ 2 (a1 a2 a3 ) = a2 a3 – a1 a3 + a1 a2
Or: C 2 = x21 + x2 2 + x23
Where: x21 = a2 a3, x22 = a1 a3, x23 = a1 a2
Which is easily remembered by defining DD 2 as the formal sum of terms obtained by dropping each a i in succession from the 2-simplex, e.g. a1 a2 a3 and taking the sign to be + if the first term is omitted and (-) if the second term is omitted, + is the third term is omitted. Referring to the preceding diagram this corresponds to going around the boundary in the direction given by the orientation arrow.
The boundary of the tetrahedron, in terms of its four faces can then be written:
We can formulate the boundary of the generic (non-ordered) 3 –simplex.
¶ 3
(
a1
a2 a3 a4
) = a2 a3 a4 – a1
a3 a4 + a1
a2 a4 – a1
a2 a3
Homology Group:
The factor group H n (X) = Z n (X) / B n (X) is the n-dimensional homology group of X.
For example, take n = 1 for a 1-simplex then we can form the quotient space:
H1 = Z1 / B 1
And re-posing the factor group by dimension (dim):
dim
H1 = dim Z1 - dim B 1
where dim Z1 = [b + 1 - n]
for any connected complex and: b = branches, n = nodes
If
we desired, we could place the points referencing the nodes into a set, which
we might call Co : the space of “zero-chains”. The “dim” or dimension measures, are very important,
and we need some of these to proceed to basic relations later:
dim C o = the number of nodes = n
dim C 1 = the number of branches = b (space of 1-chains)
dim H 1 = the number of
connected components of a complex
dim Z1 = the number of cycles = [b + 1 – n]
(For any connected complex)
Definition: The group C n (X ) of oriented n-chains of X is the free abelian group
generated by the n-simplexes of X.
Consider again the 1-simplex:
a1 ---->-----a: -----> ------ a2
Whence: ¶ 1 (a) = a2 - a1
Then we can generalize so that:
¶ n (a) Î C n-1 (X ) for n = 1, 2, 3
Similarly, we saw: ¶ o (a1) = 0 which defines a “node”
Then, since n = 0 : C -1 (X ) = {0}
Defines the trivial group of one element, or alternatively:
¶ o (a) Î C -1 (X )
Since C n (X ) is free abelian we can specify the homomorphism of such a group by giving its values on generators. For example, for n = 2,
¶ 2 (a) Î C 1 (X )
Or: C 2 = åk x i 2 i = 1
i.e.: ¶ 2 (a1 a2 a3 ) = a2 a3 – a1 a3 + a1 a2
Thus, ¶ n gives a unique boundary homomorphism denoted
by ¶ n - for which we expect mapping
C n (X ) onto C n-1
(X ) for n = 1, 2, 3.
Thus, the image of the group of (n – 1) boundaries consists
precisely of those (n – 1) chains which are boundaries of n-chains. We denote this group by:
B n-1 (X ) .
And bear in mind every boundary is a cycle.
Problem for the Math Whiz:
Consider the simplicial complex
shown below:
Given S 1 = { 1 1 , 1 2 , 1 3 }
a) Find: dim C o , dim C 1 , dim H1 , dim Z1 , dim B 1
Thence or otherwise, find: H1 = Z1 / B 1
b)Write expressions for each branch (or chain, or 1 - simplex) for the figure.
c) This (triangle space )group we can denote by B 1 (D
).
Write an expression for the 1-cycle Z 1 and thence show we may write:
¶ 1 (Z 1) = a + b + g
d) Let each node be expressed: A = 0 1 B = 0 2 C = 0 3
e) Repeat for the 1-simplexes (chains) as vectors related to the chain space C 1 :




No comments:
Post a Comment