A Caribbean Algebra II Test: Can American Students Pass It?

Having already dealt with many examples from applied Algebra II, those who followed it ought to be easily able to deal with a standard Algebra II test such as administered to Caribbean students by the Caribbean Examinations Council (CXC). Below are sample questions from a particular test. If you try this sample, allot yourself 75 minutes.

1.If (3x + 1)/3 - (x - 3)/2 = 2 + (2x - 3)/3

find the value of x

(b) Factorize completely:

 15 x² y - 20 xy²

 2) f and g are functions defined as follows:

f: x -> 3x - 5

g: x -> ½ x

a) Calculate the value of f(-3)
b) Write expressions for (i) f ^-1 (x) and (ii) g^-1 (x)
c) Hence or otherwise, write an expression for: (gf)^-1



3) Sketch  the graph of the function:   x²  + x  - 6        for:   -4 <  x <  3

Given the range of F estimate the interval of the domain for which F(x) < 0


4) Sketch the graph of the curve: y =  2x²  -  3x  - 2 

a) Using the graph find the gradient of the curve at the point where x = 2.

b) On the same axes, draw the graph of: 5y = 18x + 36

c) Using your graphs find the solutions to the simultaneous equations:

y + 2 = 2x²  -  3x  

5y = 18x  + 36


5) A car starts from rest and accelerates for 5 seconds to a point P, reaching 30 m/s. It maintains this velocity for 10 seconds.

a) Using 1 cm to represent 2 seconds on the time axis and 1 cm to represent 5 meters per second on the vertical  (velocity) axis, draw the velocity-time graph for this part of the car's journey.

b) Using your graph calculate:

i) the velocity of the car after 2 seconds

ii) the car's acceleration in the first 5 seconds

iii) The distance traveled in 15 seconds.

iv) the average speed for the 15 seconds


6) a) Given that q varies directly as p, use the values of q and p in the table below to calculate the values of a and b:

p......2........8...........a
--------------------------
q.....6.1.....b..........1.2


b) 7 pencils and 5 erasers cost $11.60, whereas 5 pencils and 3 erasers cost $7.60. Find the cost of 8 erasers.

c) If  S varies directly as (r + 1) and S = 8 when r = 3, calculate the value for r when S = 50.


7)  The floor of a room is in the shape of a rectangle. The floor is c meters long. The width of the floor is 2 meters less than its length.

a)  State, in terms of c:

i) the width of the floor

ii) the area of the floor

b) If the area of the floor is 15 m²  write down an equation in c to show this information.

(c) Use the equation to determine the width of the floor.

Teaching Algebra II The Right Way: By Applications (3)

4. Application to Newtonian Gravitational Theory:

 

A very important application of algebra is Newton's Universal law of gravitation. In one form it relates the force of attraction betweeb the mass of the Earth (M_E), say, and a smaller mass m, on its surface,  at a distance equal to its radius r:

F = G M_E m/ r²

 

If we set the weight (w =mg) equal to the force of gravitational attraction, F, we obtain:

 

mg = G M^E m/ r²

 

Or: g = GM_E/r²

 

In other words, g is independent of the mass m on the Earth's surface. Now, what about objects actually orbiting the Earth, say like artificial satellites? In this case we understand that what keeps the objects orbiting is the centripetal (or center-directed) force, which is defined as:

F_c = mv²/r

Then to achieve an orbit (say circular of radius R = r + h where h is the altitude above the surface)) we need this centripetal force F_c to equal the force of gravitational attraction, F. Or:

 

mv²/R = GM_E m/ R²

whence: v²/R = GM_E/R²

But this can be simplified even further, using the result for g above, and also using the angular velocity w = 2p/T = v/R, so:

GM_E= gr² and

mRw² = gr² m/R², so that:

 

w² = gr²/R³,

 

Example Problem:

 

Find R (= r + h), and hence h (the altitude) if the period of the satellite is known to be one day or 86,400 secs.

 

Solution:

T = 86,400s and, solving for R:

 

R = [g r²/w²]^1/3

 

R = [(10 m/s²)(6.4 x 10⁶ m)² (86400s)²)/ 4p²]^1/3

R = 4.24 x 10⁷ m = 42 400 km

But we know r = 6400 km so  h = R - r

 

And h = 42 400 km - 6400 km = 36 000 km

 

Or h » 22 500 miles above the Earth.

 

We call such an orbit geosynchronous or "geo-stationary" because the orbiting body retains an essentially fixed position above a point on the Earth and its motion (velocity) in orbit matches the rate of Earth's rotation.

To find v we have v = wr = (2p/T) r

 

= { 2p x 42.4 x 10⁶ m} / 86400 s.

 

v = 3100 m/s

 

The Newtonian gravitational law of attraction can also be extended to the Sun and any planet – say of mass m- in the solar system.  In this case, we may write:

GMm/R² = mv²/R

where R is the distance between centers. Then:

GM/ R² = v²/R 

 

Let: v = 2π/P, where P is the period

GM/R² = (2π/P)² 1/R

or, in terms of P²:

P² = (4π²/ GM) R³

which is just the Newtonian statement of Kepler’s Harmonic law.

5. Electron beam deflection:

Another intriguing application of algebra is to the deflection of an electron beam, say in a cathode ray tube such as shown. While it is true cathode ray tubes are seldom if ever used anymore, the example is still important in terms of how particles move in applied electric fields – which one may encounter, say in plasma physics. (Say with a charged particle encountering the Earth's magnetosphere.)

 

The illustration below is useful.

Deflection relates to the behavior of a beam of electrons when fired from an electron "gun" and through a defined field. The diagram accompanying shows the path of a beam through an electric field, E, set up inside a cathode ray tube.

 

Since the E-field is vertical (+ to -) as shown in the diagram, no horizontal force acts on the electron entering a region between the charged plates. Thus, the horizontal velocity component remains unaffected.

 

The displacement y in the vertical direction can be obtained from:

y = ½ at²

Then, by Newton’s second law of motion (resultant force F = mass times acceleration):

m_e a = Ee

where m_e  is the mass of the electron, E is the electric field intensity in V/m and e is the unit of electronic charge (e = 1.6 x 10^-19 C).

So the acceleration:

a = eE / m_e

Therefore, the vertical displacement can be written:

y = ½ {eE/ m_e } t²   which the student ought to see is in the same form as the kinematic equation:

 

s = ½ a t²  

so it is clear the acceleration in this case is:  a = eE/ m_e

Meanwhile, horizontally, the distance displaced is:

x = vt so t = x/v

Therefore we may write, after substituting for t in the original equation:

y = ½ (eE/ m_e) x²/v² = (eE/ 2 m_e  v²) x²

Which the student should  easily see is of the form:

y = kx² (parabola)

A special condition obtains when the electron just passes the plates (at distance x = D) so the value of y there is:

y = eE D²/ 2 m_e  v²

Then the time for transit between the plates, t is:

t = D/v

and the horizontal component of the velocity is:

v_y = a_y t = (eE/ m_e) D/v

 

 

6. Quadratic models:

 

If there’s one important equation form in Algebra II it’s the quadratic equation, of the form:

ax² + bx + c = 0

which are then solved, either by factoring and solving for x, or - very often - by using the quadratic formula:

x = [-b + {b² - 4ac}^1/2]/ 2a

Many applied mathematical models can assume the form of quadratics, so if one can solve for them one can decipher the model.

Example:

Consider the quadratic:  0.3x² + 4x + 5 = f(x)

Where f(x) is an empirical formula found to approximate the probability of a flare when a sunspot group is on or near the solar central meridian. Here: a = the proportion of largest sunspot area in the complex sunspot group or groups in relation to the total area of the complex groups., b = the number of delta class (complex) sunspot groups, and c = the total number of sunspots of large area (> 1000 msh or millionths of a solar hemisphere)  in the groups used for the formula.

Then how close to the central meridian are the groups?

 

Using the quadratic formula one gets two solutions: x1  = -1.396 and x2 = -11.937

 

Where the minus sign is take to mean the group has already passed the central meridian, and is now west of it in our line of sight. In this case the value of (-1.396) can be taken as days past central meridian, which means geo-effective flaring (i.e. causing short wave radio blackouts) is still possible.

 

7. Coordinate Equation Transformations:

 

Galilean relativity transformations are the prelude to Einsteinian special relativity. Manipulating the key quantities using algebra to get different transformational identities, is therefore a useful exercise to build algebra skills that will be needed later.

 

Basically, the interest is in how one transforms from one coordinate system, call it x, y, z to another, call it x’, y’, z’.  In the diagram below, for example, if systems S and S' are moving relative to each other,  consider a meter stick of length L (= 1 m) pointed in the +x direction and moving in that direction with velocity v. (We can also think of it as being at rest in the S' system with one end at x' = 0 and another end at x' = L', initially. )

We  look for a transformation similar to the Galilean transformation, but which will allow c (velocity of light)  to be the same in both S and S'. Since the y and z coordinates of the position are not affected by the motion in the x-direction we can say y' = y and z' = z. For the x-coordinate, we try a transformation of the form: x = a(x' + vt') and x = a(x - vt), where a is an invariant (unchanged quantity)

 

We expect a to depend on the velocity v in such a way that it becomes equal to 1 when v becomes very small compared with the speed of light. When this happens, the x and x' transformations become the same as the ordinary Galilean transformations. We begin by using x = a(x' + vt') and solve for t' and obtain:

 t' = 1/v (x/a - x')

For t' above, we now insert the value for x' (e.g. x' = a(x- vt)):

t' = 1/v(x/a - ax - avt) = at - x²(a² -1)/ va

Similarly, we find for t:

t = -at' + x'(a² - 1)/ va

Problems:

1.A beam of electrons moving with v = 1.0 x 10⁷ m/s enters midway between two horizontal plates in a direction parallel to the plates which are 5 cm long and 2 cm apart, and have a potential difference V between them. Find V, if the beam is deflected so that it just grazes the bottom plate. (Take the electron charge to mass ratio: e/ m_e = 1.8 x 10¹¹ C/kg).

 

2.A heated filament emits electrons which are accelerated to the anode by a p.d. of 500 V. Find the kinetic energy and velocity of the electron as it strikes the anode.

 

3. Given that x' = 1/a (x - vt) and t' = 1/a (t - vx/c²), derive similar equations for x and t in terms of x' and t'.  (Let: 1/a = (1 - v²/c²)^½)

If we now substitute x' = a(x - vt) and the equation for t’  into the right hand side of:

r’² = x’² + y’² + z’² - c² t’²

what do we get?

 

4. Let a quadratic model for central meridian transit of a sunspot group – indicating days past the central meridian (where the closer the value is to 0, the greater the incidence of likely flaring)  is: 

f(x) =  0.1x² + 8x + 12

 

Is this complex group more or less likely to see powerful flares than the one given in the example?

 

5. An athlete standing close to the edge on the top of a 160 ft. high building throws a baseball vertically upward. The quadratic function:

s(t) =  - 16 t² + 64t + 160

models the ball’s height above the ground, with s(t) in feet, t seconds after it’s thrown:

 

a)     After how many seconds does the ball reach its maximum height? What is the maximum height?

b)     How many seconds does it take until the ball finally hits the ground? (Round to the nearest tenth of a second)

 

6. Another form of Newton’s law of gravitation which incorporates Kepler’s third law is:

P² = 4(p)² a³/[G(M + M_p)].

where P is the planet's period, a the distance (i.e. semi-major axis, we want to solve for) and G the gravitational constant, M the mass of the Sun, and M_p the planet's mass.

Write an equation for the planet’s mass, i.e. which might be used to find it if all the parameters were known, and the units.

 

Partial Fraction Decomposition Problem:

Partial fraction decomposition uses common denominators to write a sum or difference as a single rational expression:

Add the following algebraic expressions and arrive at such a single rational expression:

3/ (x – 4)   +  2/ (x + 2)

NOTE:  Solutions to all the algebra II applied problems will appear over the next five days!

Teaching Algebra II The Right Way: By Applications! (2)

3. Simple Machines

We continue examining more applications to elicit student interest in Algebra II. The great thing about these applications, to do with simple machines, is that most can easily be constructed by the teachers to achieve a hands on effect.  We look first at a simple pulley system:

The pulley shown in 3(a) is a single movable pulley, in contrast to the Atwood machine which is a single fixed pulley. In operating such a pulley, say to lift a weight w, the force applied (F) must move twice as far as the weight w = mg. The mechanical advantage (assuming no friction) is s/d -  which is the displacement (s) of the applied force, how much it moves, divided by the distance (d)  the weight is moved. Since for Fig. 3(a) if the weight w is moved 1 m then the force F is moved 2 m. Thus, s = 2' and d = 1' so: w/F = s/d or F = wd/s = ½ w.

Example: A student sets up a pulley system using a mass of 0.5 kg which moves 0.5m. What is the displacement for an applied force F = 4N? (Take g = 10 ms^-2  )

In this case, the weight w = mg = (0.5 kg) (10 ms^-2  ) = 2 N
One needs to make the displacement s, the subject, from the equation F = wd/s.

Then: s = wd/ F  =   (2N) (0.5m)/ 4N  =   1.0 N-m/ 4N  =  0.25m

In Fig. 4A below, a variant of the earlier pulley system (a bit more complex) is depicted, called the "wheel and axle" (A) and we see also grouped pulleys (C) and multiplied strings(B). The wheel and axle is of particular interest in that it makes use of two different radii, an inner small one, r and a larger outer one R. If the depicted wheel (Fig. 4(A)) moves through one complete revolution, the distance the force will move is just d = 2πr. Meanwhile, the distance the force moves will be s = 2πR. If we take the mechanical advantage: M.A. = s/d = (2πR)/ (2πr) = R/r, then:

mg/ F = w/F = R/r and so: F = (r/R)w which is the law of the wheel and axle.
Example problem: In the wheel and axle device (Fig. 4 (A)) the radius r = 1 cm and R = 23 cm. Find the mechanical advantage and the applied force needed to lift a load of 80 N.
Solution:

In any verbal algebra problem (I or II) it is essential to identify the unknowns. In this case, we seek the applied force, F and the mechanical advantage, M.A. We also need to identify what we already know: thus load = weight = mg - 80N. R = 23 cm, and r = 1 cm.

Since: M.A. = s/d = (2πR)/ (2πr) = R/r, then:
M.A. = R/ r =  23 cm / 1 cm = 23

The applied force F can then be obtained via the ratio relationship:

w/F = R/r  =  23

Or:  F = w/23   = 80 N/ 23 = 3.47 N


Lastly, we come to perhaps the most famous machine of all, the lever. Archimedes, the ancient Greek physicist and mathematician, is quoted as saying: "Give me a lever long enough and I will move the Earth!". A basic depiction of a workable lever is shown in Figure 5.

The lever principle is applicable to everything from figuring out where two people ought to sit on a teeter totter to achieve balance, to the respective distances of two stars in a double star system, from their mutual center of gravity.

Basically a load L is placed at one end which we wish to lift by applying a force F. Let the load be a distance a from the pivot, and the applied force acts at a distance, b. Then:

Force x distance from axis = load (mg) x distance from axis or:

F x b = L x a or F = (a/b) L = (a/b) mg.

This is called the "law of the lever". It helps to illustrate using a simple problem how it works:

Example problem:

A 50 kg concrete block has to be moved from the ground to a wheelbarrow and a workman is provided with a board 5 m in length. If the workman pivots the block at 3.5 m from one end and lifts from the other (assume g = 10  ms^-2 ) What applied force is needed to lift the block? What is the work done?

We have the effort distance, a = 5.0 m - 3.5 m = 1.5 m, and the load is:

w = mg = 50 Kg (10 ms^-2 ) =  500 N, with load distance a = 3.5m.

Then, since:

F x b = L x a, we have:

F = (a/b) w and F = (1.5 m/ 3.5m) 500 N = 214 N.

The work done is

Fs = (mg)d but (d/s) = (a/b)


 so Fs = (a/b) mg x 1.5 m = 321 J.


Additional problems:

1. a) In the grouped pulley system depicted in Fig. 4 (C) the force applied F will move 6 times as far as the load w. If the load has a mass of 40 kg, and assuming g = 9.80 ms^-2, find the applied force. Thence or otherwise, obtain the mechanical advantage of the system. If the force F is applied through 10 m what is the work done? (Work is defined as the force times the distance moved, i.e. against gravity, or W = F x)

b) Examine the pulley system shown in Fig. 3(b). How would the basic applied equation for force and mechanical advantage be changed compared to the pulley shown in Fig. 3(a)? (Given that:  F = wd/s = ½ w  for the single moveable pulley in 3(a))


2. A man raises a uniform plank 12' long and of weight 40 lbs. until it is horizontal. His left hand is on one end of the plank and his right hand is 3' from the same end. Assuming both hands exert vertical forces, find the forces exerted by each hand to support the plank.

3. In the sample lever problem it is feasible to reduce the work done to only 125 J by re-arranging the lever distances (effort and load distance). Using a sketch show how could this could be done and give the new applied force in this scenario.

4. The "line of centers" for a binary star orbit, in reference to the center of mass x, is shown below:

A O------------x cm-------------------------o B

The sum of the two stellar masses is given by:

m(A) + m(B) = 3.2 M_s

where M_s   denotes solar mass units.  If mass  m(B) = ½ m(A)  then find the distances Ax and Bx. Thence also find the masses of m(A) and m(B) in terms of solar masses (M_s ).


5. The sum of masses for a binary star system can also be obtained using Kepler's 3rd law:

m1 + m2 = a³/P²


Using this, where a = the separation of the stars in astronomical units (AU) , and P is the period for their revolution about the center of mass in years, find P if:

m1 + m2 =  1.8 solar masses and a = 0.16 AU.

TEACHING ALGEBRA II THE RIGHT WAY! USING APPLICATIONS!

According to the author of the HARPERS piece ‘Wrong Answer’, one gripe of Algebra II students is the ‘bait and switch’ tactics often used in their textbooks. The author cites a caption introducing Chapter 8 of the Algebra II Common Core text which displays a Basilisk lizard racing across the surface of a body of water – and there’s a hint (in the caption) of applying algebra to find the “surface tension” and application  – but nothing manifests. It’s a dead end!

The author, Nicholson Baker,  then exposes the scam:

“There’s nothing about surface tension or walking on water in Chapter 8, and indeed the caption would puzzle an expert on reptilian locomotion- since basilisk lizards don’t actually rely on surface tension to run on water. They’re like heavy striders”

He then goes on to explain the real physics, which attributes the lizards’ water skimming ability to “relying on the momentary inertia of the boluses of water beneath its long toed feet.”  In other words, certain discrete semi-separate masses of water (boluses) possess the property of inertia (resistance to displacement) when the reptile scampers over them – thereby allowing it to appear to skim the surface of the water if fast enough. But again, no algebra is shown to be applied.
 

Instead of teaching slavishly (and abstractly – i.e. via formal definitions), to a text, why aren’t various applications emphasized to really get students engaged? In this and two more blogs I will show a variety of ways to apply algebra to drum up of the interest of Algebra II students.  Each application requires only a passing or basic introduction to certain algebraic principles without going hog wild into abstraction, i.e. trying to get a kid to differentiate between continuous and non-continuous rational functions. In the case of an applications –based course, the question of whether functions employed are continuous will arise naturally – say in the course of discussions, or the applications.

 

 

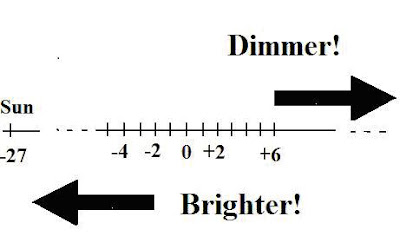
1. Application to the Number Line:
 

One of the foremost concepts any student of algebra needs to master is the number line. There have been various ways to present it, but the most sterile is the teacher simply drawing a boring line on a blackboard and filling in numbers - positive and negative- at regular intervals. A better way is to introduce an immediate application, which demands the use of such numbers - say the stellar magnitude scale shown above.

 

 

If the students are told there is a way to tell the brightness of one star from another, they ought to immediately become curious. You then let them know the brightest stars are assigned negative numbers and the less bright positive ones. A class exercise would be to mark out an extended magnitude scale, say from (-26.5) at one end, to maybe +10 or +15  at the other. You can then use a star atlas to write the stellar magnitudes on the board - or on whatever medium is applicable - and let the kids fill them in.

 

 2. Kinematic applications:
 

Number line too boring?

 

Then one can really get into the 'nitty gritty' with the application to kinematics and dynamics. In this case, the motion of some object, say motor vehicle, is recorded on a distance - time or other (velocity v. time) graph, such as shown below and the results interpreted.

The top graph gives the displacement s in terms of the time as: s = 2t. The bottom graph gives the velocity based on this motion, which will be: v = s/t = 2t/t = 2, say in meters per second. Since there is no initial velocity, u = 0, then (v – u)/ t = 0 and the slope the v-t graph is zero. Meanwhile, the graph of the s-t graph (top) has constant slope. In either of these instances one can infer there is uniform motion and hence Newton’s 1^st law of motion applies.

 

 

 The basic equations of kinematics can then be derived or given, allowing all sort of interesting problems to be worked out. These equations include:

 

 

1) v = u + at

 

 

which relates the final velocity to u, the initial velocity and then to the acceleration a and time it is in motion, t.

 

2) s = ut +  ½ at²

 

This relates the distance traveled to the initial velocity u, the time t, and any acceleration a, If the initial velocity u = 0 then, s = ½ at²

3) v²  =  u²   + 2as
 

A different form relating final velocity to initial velocity u, and distance covered, as well as acceleration.  Remember, that when one moves on to calculus, the primary bugbear of all students is algebraic manipulation (say using partial fraction decomposition),  not recalling continuous and discontinuous functions and their properties.  A good exercise for students is to change the subjects for the different kinematic equations, which the teacher can propose for different circumstances.

 

For example, take equation (2). Now, apply it to a falling body, say a rock, dropped from a tree 20 m high. Then we know s = 20 m, and the initial velocity u = 0. So, how long it will it take to reach the ground? You need to solve for t, the time. (You can take g = 10 ms^-2  to keep it simple, or use 9.8 ms^-2 .)

 

 

In the case of equation (3) maybe a car initially moving at 30 m/s brakes to 10 m/s and does so in two seconds. How would you find the deceleration a? Would you need more than one kinematic equation to find it?

 

 

Application problems:
 

 

1) A car moves at 10 m/s for a period of 5 seconds then slows to 5 m/s for the next 10 seconds. Draw a graph showing the complete motion. What is the speed of the car after 2.5 seconds? What is its speed after 8 seconds? What is the total distance covered over 15 seconds? Over the first 5 seconds?

 

 

2) A go Kart starts off with an initial uniform velocity of 2 m/s for 5 s. It then accelerates to 3 m/s in 1 second and sustains that for 3 seconds. What is the distance it covers?

 

3) A car is traveling along a level road at 50 km/h, then it speeds up to 80 km/h over a period of 5 minutes. Find the acceleration in m/s/s and the distance covered in the time, in m if it maintains the final velocity for 1 minute. (Take 1000 m = 1 km, 1 h = 3600 s)

Kids Hate Algebra II? WHY?

Quick! Do the following in 10 minutes or less!

If (3x + 1)/3 - (x - 3)/2 = 2 + (2x - 3)/3

find the value of x

(b) Factorize completely:

(i) 15 x² - 20 xy²

(ii) 3 - 12b²

2) f and g are functions defined as follows:

f: x -> 3x - 5

g: x -> ½ x

a) Calculate the value of f(-3)
b) Write expressions for (i) f ^-1 (x) and (ii) g^-1 (x)


3) Solve the quadratic equation:

x ²   -  3x  + 2= 0

Plot the graph, indicating the coordinates of any maximum (or minimum), and also of any x-, y- axis intercepts.


If you were able to complete the above problems, even if not necessarily in the time, then you likely took Algebra II.  If not, then well, you obviously stopped at Algebra I, assuming you took Algebra at all.

Now, however, it's come to light that kids HATE Algebra II! They are sick and tired of it and want out. This according to the article 'Wrong Answer!' in Harpers (Sept., p. 31) by Nicholson Baker. The author provides a number of examples of Algebra II hate he encountered on the Web with comments such as:

"Algebra needs to die!"

"Is poking myself in the eye an acceptable substitute for my algebra homework?"

"Algebra is the huge fucking dam that prevents me from flowing, and being a better person!"

"I have to take 11 algebra tests in 2 hours. It's six in the morning and I've got to pass 'em all or I fail!"

"I really hate Algebra 2! I wish I was dead! I want to kill myself!"

Woah!  Can it be THAT bad? What's going on?  Why are all these kids so miserable and some, evidently, to the point of phoning it in (though granted we must make allowances for teen hyperbole!) The author, Baker, believes he has the answer: It's the Algebra 2 Common Core, stupid! Egged on by the ridiculous 'race to the top' baloney (which only rewards a few schools anyway), schools across the nation have evidently adopted a new, common core Algebra text by Pearson which:

"is very new and very heavy"

Also:

"The federal Race to the Top grants have encouraged your school to buy many copies of this new, expensive textbook along with the associated workbooks and software licenses."

For what? Well, evidently in order to follow the injunctions of the "Common Core" standards developed by a non-profit outfit called Achieve, "and paid for by grants from the Bill and Melinda Gates Foundation".  Baker then quotes Melinda Gates:

"High standards mean more than just teaching all students Algebra II. It means teaching all students the skills necessary for success in Algebra II so they can apply them in different areas throughout their lives and careers."

In other words, Melinda - and likely Bill too- are convinced that a high standard of performance in Algebra II will translate to major useful life-career skills.  But I dispute this, and so does Baker, and so does a high profile mathematician, Underwood Dudley - a number theorist who for many years has been  a sharp critic of required math courses. As Dudley put it in an issue of The American Mathematical Monthly in 1987:

"The vast majority of the human race and the vast majority of the college educated human race never need any mathematics beyond arithmetic to survive successfully."

Wow! What a transgressive statement! It basically turns the entire Common Core Algebra II standards idiocy on its head. He's saying that not only will the college -educated barely use the math embodied in Algebra II, but for sure neither will those with just high school degrees. I mean hell, you don't need Algebra II to work out how much interest you will have to pay on your 4.5% mortgage on a $150,000 home (for which you paid $20,000 down) over thirty years.  You don't need it to figure out a 20% saving on a pair of jeans that normally costs $19.99 - and factoring in a 5% tax.

Obviously, having said all that, it doesn't apply if a kid plans to go into engineering or astrophysics. Then, he will need not only Algebra  II but plenty of calculus, as well as differential equations, numerical analysis and complex analysis. But how many college grads will go that STEM route? Better, how many graduating with a STEM degree will actually find a STEM job?

The author also makes the cogent case that if thinking skills are really what's required, Algebra II isn't essential to specifically fulfill the need. Many alternatives can be found, e.g. a basic logic or critical thinking course. So, why in hell expose so many kids to stuff like rational functions, as defined e.g. in  Chapter 8 of Algebra 2, Common Core:

"A rational function is a function that you can write in the form: f(x) = P(x)/Q(x) where P(x) and Q(x) are polynomial functions. The domain of f(x) is all real numbers except those for which Q(x) = 0"

The author adds: "Not only that but rational functions can be continuous or discontinuous, and a continuous rational function is one that 'has no jumps, breaks or holes'"

To make his point further, on how the average non-math oriented kid can be confused:

"Next you're presented with a salient feature of discontinuous functions: If a is a real number for which the denominator of a rational function f(x) is zero, then a is not in the domain of f(x). The graph of f(x) is not continuous at x = a and the function has a point of discontinuity at x = 1.

Then you learn something more about points of discontinuity: they can be either removable or non-removable."

Got that? If you don't, then imagine some kid who isn't math savvy sitting for endless hours a week in a classroom and getting more frustrated with each succeeding lesson. Imagine the frustrated teacher that has to teach this to a class, to whom it comes over as Greek, literally. Then you get the picture of why forced Algebra II for a mass audience, a mass captive high school audience, is a bad idea.

As for the textbook:

"Algebra 2 Common Core is, in other words... a highly efficient engine for the creation of math rage: a dead scrap heap of repellent terminology, a collection of spiky, decontextualized, multi-step mathematical black box techniques that you must practice over and over..."

As it is, all our schools are going under the spell of this 'Common Core' BS -  and it's creating mass hatred of math. We have kids actually talking of killing themselves over it, or else expressing such manifest hate that they will be math detractors for the rest of their lives.  This is not the way to move the nation forward educationally.

We can do better and have to do better. It's time to rethink the standardization of high school math and realize we can't fit 22 million square pegs into 22 million round holes. In the words of Underwood Dudley, in his math article (ibid.)

"We cannot justify teaching mathematics to 17, 18-year olds by asserting they will find it useful. We cannot claim we are presenting beauty either. We are, of course, but what percentage of our students can see that, however dimly?"

He thereby pigeonholes the problem in a nutshell. As Nicholson Baker puts it:

"If Algebra II were an elective and colleges didn't ubiquitously demand it, fewer people would learn it. But fewer people would fail it too, and fewer people might drop out of high school, and the level of cheating would go down, and the sum total of student misery would be reduced."

Words to consider!