Stellar Line Formation and Transitions (3): Complex Atoms

  L-S coupling - which we had seen in a 2014 post, e.g.

An Introduction to Quantum Mechanics (2)

plays a major role in quantum processes and spectral line formation. Here we consider more on formation of spectral lines based on electronic configurations in complex atoms. To fix ideas, all the configurations to be considered obey L-S coupling with energies ordered by the LS –value. However, each is split according to the quantum number J = L + S.

The energy of a complex atom can be expressed:

 E  =  

å^N _{i = 1} {p _i ²/ 2m  -  Ze² / r _i   +  e _i (r _i ) L _i S _i  }+

å^N _{i>j = 1}  e² / r _ij  

     Where the large bracketed quantity is the hydrogenic energy, composed of the kinetic energy (first term), the nuclear attraction (second term) and the spin-orbit interaction. The second term (unbracketed) is the electrostatic repulsion from the other electrons

     Note in what follows that we typically use the uppercase letters (L, S, J) for the momenta of the whole atom and reference lower case letters (ℓ, s, j) to individual electrons. In general the quantum numbers, e.g. LS, denote the term which has a given multiplicity, 2S + 1.

Thus the terms in less than half-filled shells are ordered according to J. (Recall a collection of orbitals under the same value of n is called a "shell". Thus, for n = 4, we have ℓ =0, ℓ = 1, ℓ =2, ℓ = 3 so comprising the collection of orbitals: s, p, d and f.)

 Thus for the case:  L = 3  and  S = 1/2

J = 5/2    

     Recall that a spin-orbit interaction results with a total angular momentum J’ = L’ + S’, where L’ denotes total angular momentum = L1 + L2 etc.

L’ = Ö{l’ (l’ + 1)} h,

and S’ the total spin angular momentum = S1 + S2 etc.

S’= Ö{s’ (s’ + 1)} h,

Then: J’ = Ö{j’ (j’ + 1)} h.

 One applies these to a particular atomic configuration, say: 2p 3d then goes through a procedure of taking differences, assigning values etc. based on selection rules. 

 For the configuration given, one particular energy level occurs for:  

s’ = 1 (s’ = ½  + ½)  and:  l’ = 1  (l’ = ï1-2ï)

for which j’ = 2, 1 and 0.

Meanwhile, the term S = ½, L = 2 is written ²D and is referred to a “doublet D”. The total angular momentum J specifies a level and the multiplicity indicates how many level are possible. For example, ²D_5/2  is the level of doublet D with J = 5/2.

 A ‘triplet’ spectral line can also appear – which might be depicted in a diagram with energy states ³P₂, ³P₁, and ³P₀. The capital letter (P) denotes one of several energy levels given by S, P, D and F, etc., corresponding to values of the quantum number  l = (0, 1, 2, 3 etc.) in an ascending alphabetical order from F. 

 Hence, l’ = 1 implies P-level, and the subscripts denote J’ =  0, 1, 2 values. The superscript ‘3’ is the multiplicity, derived from the relation: 2s’ + 1 = 2(1) + 1 = 3, employing the spin quantum number.  Note carefully the j’ values seen for the differing energy levels in the diagram below:

 For more than half-filled shells the levels of highest J lie lowest. But if there is no configuration interaction, the spacing between the adjacent levels is proportional to the greater J-value.  The number of electrons in each n ℓ shell is given by raising the ℓ to that power.

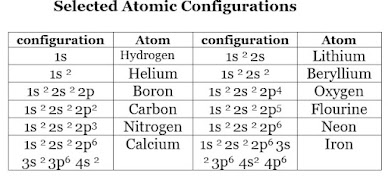
Thus, 2p⁵   as shown in the Table below for atomic configurations, means 5 electrons in the 2p shell. 

                                                                       

Recall that because of the Pauli Exclusion Principle no two electrons may have the same quantum number, so the values ℓ, s, m _ℓ,  m _s  must be different for each electron.)   Since  m _ℓ  has 2 ℓ + 1 values and m _s  has two, then electrons can occupy each shell.

Let’s now consider a more complex LS –coupling configuration for nd n’p. For which we may ascertain: n = n’, ℓ = 3, s’ = 0, 1 and ℓ’ = 1, 2, 3. 

                                                                

The splitting of this single degenerate energy level – with two optically active electrons – is due to the residual Coulomb repulsive force and the spin –orbit perturbation. While it’s not possible to write explicit equations for which the energies of all levels can be computed, we can write and equation that gives the j’ dependence of the spin –orbit interaction energy.

 DE _S.L =  

 h²/ 4 π  m_e c²   1/r( dV(r)/dr)[j(j+1) - ℓ(ℓ+1) – s(s+1)]

Bearing in mind the procedure for how we obtain the S, L, J values from the spectroscopic notation, say ³ D ₃ where the superscript is given by 2S +1, and the subscript by J with the L –value corresponding to the letter value from the table:

Value  of L	0	1	2	3	4	5
Symbol	S	P	D	F	G	H

Then: 2S + 1 = 3 so that: 2S = 2 and S = 1

While: J = 3 and L = 2.  Hence:

L·S    =  ½  [3(3+1) - 2(2+1) – 1(1+1)] ħ ²

L·S    =  ½  [3(4) - 2(3) – 1(2)] ħ ²

L·S    =  ½  [12 - 6 – 2] ħ ²  =  ½  [4] ħ ²

=  2 ħ ²

While the preceding was written for an atom with one optically active electron, it can be recast using primes to give the interaction energy for the total spin and angular momentum vectors S’ and L’, of any atom for which LS coupling is valid. Thus, we may write for greater generality:

DE _S.L =  K [j(j+1) - ℓ(ℓ+1) – s(s+1)]

Where: K = h²/ 4 π  m_e c²   1/r ( dV(r)/dr)

And K has the same value for all energy levels with the same values of s’ and ℓ’.

More typically, K is found from the difference in LS values between levels, such that:

DE _S.L =  K (L·S )_upper - K (L·S )_lower 

Suggested Problems:

1) Enumerate the possible values of j and m _J for the states in which ℓ = 1 and s = 1/2 and draw the associated vector diagrams.

2) Consider an electron for which n = 4, ℓ = 3, and m _ℓ = 3. Calculate:

a) the numerical value of L, the total orbital angular momentum

b) the z-component of the orbital angular momentum.

3) A two-electron atom for which the orbital angular momentum quantum numbers are ℓ1 =3 and ℓ2 = 2 can have what values for the total orbital angular momentum number L?  Determine the possible values of the total angular momentum quantum number of single f  electron.