An Introduction To Differential Geometry - Part 6

 Overview Of Tensors & Operatioins:

Since this part of differential geometry will initiate the use of tensors we begin by going through some preliminaries.  Those readers who've not yet been exposed to tensor algebra can access some examples here:

• Looking At Some Basic Operations & Computations In.Tensor Algebra..

We have already seen, experienced, developed multiple occasions to use vectors, i.e.

• Revisiting Vectors And Solid Geometry (Part 1)

But all such vectors are just tensors of rank 1.

By extension, a tensor of rank 2 (e.g. moment of inertia tensor I _i j ):

  I _{i j}  =  m [x ²   d _{i j}     -  x _j  x _j  ]

is a dyad.

The most basic tensor of all is the unit tensor, defined:

1  =  i^ i^ + j^ j^ + k^ k^  =

(1......0........0) 

(0........1.......0)

(0........0.......1)

Also:

1 × C  =  i^ C_x + j^ C_y + k^ C_z  

Further properties:

A tensor is symmetric if:  T _{i j}   = T _{j i}

A tensor is anti- symmetric if:  T _{i j}   = -  T _ji

The latter will look something like this:

(0 ……a₁₂………a ₁₃)

(-a₁₂…..0……….a₂₃)

(- a₁₃……-a₂₃……0)

The fundamental  metric tensor : g _mn  or    g _ab  *   is of special importance in differential geometry. Thus

g _mn  =  g _ab = 

(g ₁₁      g ₁₂      g ₁₃           g ₁₄ )
(g ₂₁     - g ₂₂     g ₂₃         g ₂₄)
(g ₃₁       g ₃₂      g ₃₃        g ₃₄ )
(g ₄₁        g ₄₂       g ₄₃      g ₄₄)

A metric which is defined by a quadratic differential form, e.g.

ds²   =  å ⁿ m ₌₁   å ⁿ _v =1 g _mn du ^m du ⁿ

Or:

ds²   =  å ⁿ _a =1   å ⁿ _b =1 g _ab du ^a du ^b

Is called a Riemannian metric.  This references a general case in which we have introduced n real dimensions, u¹,  u ²   … u ⁿ   in order to obtain a Riemannian space.  Going forward we will also use an abbreviated summation convention, e.g.

ds²   = g _ab du ^a du ^b

or:  ds²   = g _mn du ^m du ⁿ

Fundamental forms:

A quadratic form: 

F(x,y) =  a ₁₁ x ² +  2  a ₁₂  xy +  a ₂₂ y ² 

Of two real variables x and y is called positive definite if it has a positive value for any pair (x, y)  ≠   (0, 0)  At regular points on a surface if these are consistently positive definite we expect a 'first fundamental form'

A curve on some surface  S,: x ( u¹ ,  u ² )   can be determined by a parametric representation, i.e.  u¹ =   u¹(t),   u ²  =   u²(t)

Where the parameter t is a real variable.

Example: Any circular helix;  x(t) = (r cos t, r sin t, ct) 

is a curve on a surface S and can be represented by:

 u¹ = t,    u ²  = ct    or as:  u ²  = cu¹ 

Of particular importance in differential geometry are the coordinate curves:  u¹ = const.,   u ²  = const.  on a surface S: x ( u¹ ,  u ² ).  These correspond to parallels to the coordinate axes in the  u¹  u ² -plane.  (Refer back to Part 5).  A set of curves on a surface S which depend continuously on a real parameter is said to be a one parameter family of curves on S.  For example a family of parabolas on a Cartesian surface,

A family of curves can also be determined by a suitable linear differential equation of first order, e.g.

dy/ dx = f(x,y)

Or:   du ²/ du¹     =  F  (u¹ , u ² )

The direction of the tangent to a curve on a surface S: x ( u¹ ,  u ² )   is determined by the vector: 

x' =  dx/dt =  (¶ x /¶ u¹ )   du¹ /  dt  +  (¶ x /¶ u² )   du² /  dt =

x ₁ u^1'  +  x ₂  / u²

Which in general depends on t.  Note the vector x is a linear combination of the vectors x ₁  and x ₂ .

More generally, the first fundamental form is always associated with a Riemannian geometry.  We already saw:  

u¹ =   u¹(t),   u ²  =   u²(t)

It is instructive here to determine the element of arc of such a curve which leads in a practical application to the first fundamental form.  We have seen above the summation form:

ds²   =  å ⁿ _a =1   å ⁿ _b =1 g _ab du ^a du ^b

From which we can also write:  x _a · x _b  = g _ab

which leads to:

x ₁  ·  x ₁ = g₁₁             x ₁  ·  x ₂ = g₁₂           x ₂  ·  x ₁ = g₂₁

And:    x ₂ ·  x ₂ = g ₂₂

And the resulting full quadratic form:

ds²   = g₁₁ (du¹)²   + 2 g₁₂ du¹ du²  + g₂₂ (du²)² 

Is called the first fundamental form.

Example Problem:  Let a sphere be represented by:

x ( u¹ ,  u ² ) =  (r cos u ²  cos u¹ , r cos u ² sin u¹ , r sin  u ²)

Find the first fundamental form corresponding to this representation:

Soln.  

 The first partial derivatives are;

 x ₁    = (- r cos u ²  sin u¹ , r cos u ² sin u¹ , 0 )

x ₂   = (- r sin u ²  cos u¹ , - r sin u ² sin u¹ , r cos u ² )

This yields:  x ₁  ·  x ₁ =  r² cos  ² u ²

x ₁  ·  x ₂ = g₁₂ = 0   And:   x ₂ ·  x ₂ = g ₂₂  = r ²

Then the first fundamental form corresponding to the sphere as represented is:  

ds²   = r² cos  ² u ² (du¹)² + r ² (du²)² 

Suggested Problems:

1)  Find the first fundamental form of the cylinder: 

x ( u¹ ,  u ² ) =  ( h ₁ (u¹), h ₂ (u¹),  u ²)

2) Find the first fundamental forms corresponding to Cartesian and spherical coordinates in space.  

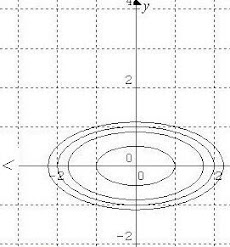
 3) What differential equation would give rise to the family of curves shown below?