In Earth’s upper ionosphere, magnetosphere and solar wind, the collisional mean
free path is large, so the plasma is collisionless and often far from thermal equilibrium. See my earlier post on collisional and collisionless plasmas, e.g.
Standard collisionless fluid
equations and energy transport equations can be derived for constituent species by taking
velocity moments of the Vlasov eqn. for each species. The moment equations are expressed in terms of (standard) velocity moments of
the particle distribution, f(v). In collisionless space-plasma fluid equations there are no
electron-ion collisions and there is no collisional conductivity. Energy transport can only
occur by convection, described in terms of particle energy fluxes or by radiation.
As reported in EOS: Earth & Space Science, (March, p. 44) M.V. Goldman et al - in a new paper ('Multibeam Energy Moments of Multibeam Particle Velocity Distributions') appearing in Journal of Geophysical Research: Space Physics:
https://doi.org/10.1029/2020JA028340
have presented a novel method to treat space plasmas using multibeam velocity components for a measured plasma distribution. The approach allows a better understanding of how much of the system's fluid energy is kinetic and how uch is thermal (ie. associated with velocity fluctuations about the primary beam flow velocity, u. The authors suggest that a multibeam approach offers clear advantages when interpreting energy transport in complex plasmas, although they note that the approach is based on assumptions, such as the number of beams into which a given distribution should be decomposed. In this post I examine the multibeam concept as laid out in their paper with the view to better grasping the importance of their work.
We first note there are other terms in the standard collisionless fluid equations that resemble those in the collisional
fluid equations. This is even though f(v) is not generally Maxwellian. For a given f(v) there is one flow
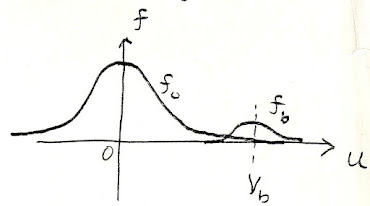
coherent velocity, u and one mean number density, n. An illustration of a dual beam system from a previous blog post is shown below:
Note that higher-order moments decompose into a sum of a
coherent part (involving u) and an incoherent (“thermal”) corresponding to moments of
velocity fluctuations, which can be written out as:
ò d3 v f(v)|v – u|2//2 or: ò d3 v f(v) (v – u) |v – u|2.
Thus, the energy density of a given species is the sum of a bulk kinetic energy density, nmu2//2, and a thermal energy density moment, m ò d3 v f(v)|v – u|2//2 ; the energy density flux is a sum of a coherent bulk kinetic energy flux, unmu2 /2, and a “thermal” energy flux moment (enthalpy plus heat flux).
Goldman et al note that meaning of each of the decomposed moments is well understood and not
controversial for contiguous and effectively single-peaked velocity distributions, f(v). However,
for multibeam (effectively disjoint) f(v), standard velocity moments can give rise to
misinterpretations such as false identifications of incoherent energy density and temperature. Also, because their velocities cancel out when averaged, single fluid moments can appear to contain all thermal energy and no (bulk) kinetic energy - leading to misinterpretation.
In Goldman et al's paper an alternate method is developed for taking velocity moments of an N-beam velocity
distribution, f(v), of form f(v) = f1(v) + f2(v) + … + f N(v). Such multibeam moments are formed
by taking standard coherent moments or standard thermal moments of each beam, f j(v) and then
summing over beams j = 1 to N. It is important to note that the sum of the coherent plus the
“thermal” parts of a higher-order moment remains the same whether the velocity moments are 4
standard or multibeam. Such a sum will be called an undecomposed higher-order moment.
An
example is the undecomposed particle energy density, nm<|v|2 >/2, which can be decomposed by
writing:
v = u + (v – u) In practical space plasma applications f(v) is measured by electrostatic analyzer
instruments
The ion and electron velocity distributions, f(v), consist of a
number of effectively disjoint pieces in velocity space, which the authors refer to as "beams". This
calls into question the use of standard moments because experimentally the distribution is not
contiguous; nor is it single peaked. In particular, difficulties of interpretation may arise, and the
underlying physics may become obscured by using a description which does not adequately
capture the phenomena being observed.
Consequently, for the multibeam f(v) portrayal it is more useful not to take moments in the
standard way but rather to take standard decomposed moments beam by beam and then add
them together. The authors call such sums multibeam moments.
The authors' diagram below shows two equal and opposite cold electron beams, with
velocities u o and -u o and equal densities n o. According to standard
moment theory the effective velocity distribution, f(v) is one entity,
with one flow velocity, u. In this example, u = 0, so the bulk kinetic
energy moment, U (bulk) is zero and the (single) density is n = 2n o.
The
incoherent energy density moment found from standard moment
theory is mn(u o) 2 /2. This incoherent part of the energy density is
often called the thermal energy density and written as U(therm) = nT'.
This yields an effective temperature, T ' = m(u o) 2 /2. The authors provide the following cautionary note:
"A difficulty
with such a standard moment is that the pair of cold moving beams
appears to have a temperature, which we will call here a false temperature, T' but no bulk kinetic energy density.
This is customarily remedied by simply considering f(v) to be a two-beam system, f(v) =
f1(v) + f2(v)."
(Or as I indicated in the earlier diagram: f(v) = f o + f b .)
The density and velocity moments of f1 and f2 are {n1, u1} and {n2, u2}, where, n1 =
n2 = n o , u1 = u o and u2 = - u o. The energy moments of each beam are now U(bulk)1,2 = n o m(u o) 2 /2
and U(therm)1,2 = 0.
For the system of two beams, (Ubulk)
2-beam = Ubulk1 + Ubulk2 = n m(u o) 2 /2, where n
= n1 + n2 = 2n o and (Utherm)
2-beam = 0 + 0, which is more intuitive than the results of the standard
moment analysis, with respective velocities: U(bulk) = 0 and U(therm) = nm(u o)2 /2.
Goldman et al summarize their results for the two different ways of taking energy moments of f(v) =
f1(v) + f2(v) in their table below:
It is hoped that this preliminary introduction into multiple velocity moments, using the authors' own formalism, will aid readers in getting more out of the excellent JGR paper referenced with the doi citation above.


No comments:
Post a Comment