We know the standard model of Big Bang cosmology, known as ΛCDM, incorporates how the assorted cosmological components outwardly behave. Dark energy, the model presumes,
Takes the form of a cosmological constant Λ, or a constant energy density per unit volume of vacuum. And dark matter is cold—that is, nonrelativistic—and interacts only via gravity and possibly the weak force.
Now it turns out (Phys. Today, March, p. 14) discrepancies are showing up in the measurements of the Hubble constant H0 - based on gravitational lensing techniques. To fix ideas, the ΛCDM model predicts that the universe today should be expanding at a rate of 67.4 ± 0.5 km/s/Mpc. But a direct measurement of H0 based on observations of standard candles—Cepheid variable stars (e.g. Measuring Stellar and Celestial Distances )
And type Ia supernovae—give a different value: 74.0 ± 1.4 km/s/Mpc.
Now we learn that new collaborative research led by Sherry Suyu, from H0LiCOW (H0 Lenses in COSMOGRAIL’s Wellspring) uses gravitationally lensed quasars to independently measure H0. The group’s latest result, 73.3 + 1.7 − 1.8 km/s/Mpc, agrees well with the standard-candle value. Combining the H0LiCOW and standard-candle measurements gives an H0 of 73.8 ± 1.1 km/s/Mpc, which differs from the ΛCDM value by 5.3 standard deviations.
As I noted in a previous blog post e.g
Arriving at a More Refined Hubble Constant
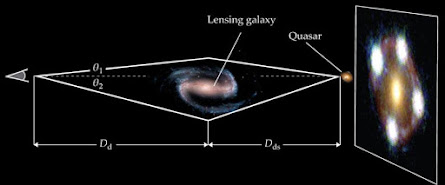
There has been ongoing work on improving the value of such as described in the link to an Astrophysical Journal preprint paper in the above blog post link. In the current research related to the H0LiCOW work, it is crucial to note the link to a theoretical basis called "time delay cosmography". Reference to the graphic shown (compliment of Freddie Pagani, ibid.) can be instructive in understanding how the gravitational lensing works.
Basically, when a quasar or other luminous distant object lies in the line of sight of massive object, i.e foreground galaxy, its light is deflected so strongly that multiple images appear (see the extreme right frame of the graphic)
The challenge in any direct measurement of H0 is in gauging the distances to faraway astronomical objects; their velocities relative to Earth, in contrast, are readily inferred from the redshifting of their radiation. Standard candles are appealing because their luminosities are known, so their distances can be calculated from how bright they appear on Earth. In H0LiCOW’s complementary measurement, the researchers studied quasars whose light is so strongly deflected by foreground galaxies that they appear as multiple distinct images, as shown in the figure. Because the light in each image traverses a path of a different length, fluctuations in the quasar’s light show up in the lensed images at different times.
Measuring those time differences, which are on the order of weeks, doesn’t directly yield Dd (the distance from Earth to the lens) or Dds (the distance from the lens to the quasar). But it does constrain their combination, which is enough information to calculate H0 from the objects’ known redshifts. In 2017 the collaboration published a first result based on three lensed quasars (see Physics Today, April 2017, page 24). The current work extends the analysis to six quasars. Below are shown the light curves from four lensed images of the quasar shown in the top graphic.
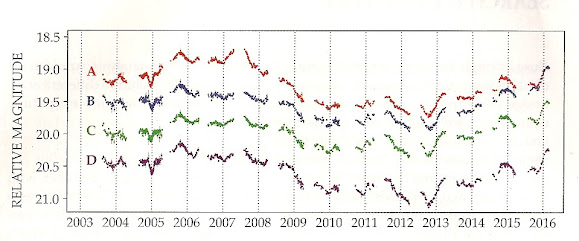
These curves were collected over 13 years from the COSMOGRAIL collaboration. Note that fluctuations in the quasar's intensity appear first in the curves A and C, then in light curve B. Finally, two weeks later in light curve D. The key point is that sufficient information is obtained - using 1 to 2 m telescopes- to get H0.
Basically, given the two angles, q1 and q2 are small, the difference in path lengths shown(top graphic) will be proportional to: (Dd Ds )/ Dds . Here the denominator refers to the distance from the galaxy to the quasar. Now, the difference in light travel time, which includes the effects of general relativity and the cosmic expansion, is proportional to the same value. Recall in the case of general relativity, we are looking at the deflection of light as a result of encountering a massive object along its path, e.g.
We can obtain for the deflection angle, :
a = - 4 GM/ b or (in cgs units):
a = - 4 GM/ b c2
Finally, in obtaining H0 we note the importance of the lensing galaxy's mass distribution. This is needed to calculate the deflection angles, q1 and q2 .These, again, are analogous to the angle a computed in the example above.
These results in tandem lessen the likelihood that the H0 discrepancy is due to some unappreciated systematic uncertainty in the standard-candle measurement. Taken at face value, they seem to point toward a need to revise the ΛCDM (Standard) model.
For those interested in further details, see: K. C. Wong et al., Mon. Not. R. Astron. Soc., in press, https://arxiv.org/abs/1907.04869.)
No comments:
Post a Comment