A Problem Template For Pendulum Libration , Simple Harmonic Motion & Total Energy

 

  Simple Pendulum:  At angle q  the motion is not simple harmonic.

Consider  the equation for a simple pendulum:

d ² q / dt ² =   - k sin  q

 If  q  is small enough i.e. sin q »   q 

Then: d ² q / dt ² =   - w ² q

 or:   q ^" =   - w ² q

So the problem reduces to one of SHM.

We can also formulate:

ò ( d  q / dt  ) (d ² q / dt ²   ) =  ½ ( d  q / dt  )

= -  ò w ² sin  q (d q / dt ) =   w ² cos  q +  C

Now define: f =  q /2 =    ò ÖA dt = ò d f/ [Ö1 - k sin  ² f ]

 Since:

Cases:

i) For k = 0,  w = 0, trivial

ii) For 0 > k > 1,  f  can take on any value.

iii) For k = 1i: Integrand ® oo  when f  ®  p /2

iv) For k > 1: Integrand exists for sin  ² f  <   1/ k 

Since: 1 - k sin  ² f  > 0

We then have the condition for libration that: k > 1

In effect,  k is a function of total energy of the system k (w², C). A graph of the latter  (as potential energy V( q )) through the motion in the plane is shown below:

At the libration level we see the motion of the pendulum is constrained i.e. between two 'mirror' values for q:

For q :    - 2 a   <   0   <   2 a                 0   <   2 a  <   2p 

For this energy E  less than a certain critical value (E crit = 2 mgL), the pendulum will just swing back and forth in the plane.  ( The critical value of E is just the value of the potential energy at the top, q = ±p) This kind of periodic motion is called libration. 

 In contrast, if E is greater than the critical value, the pendulum will swing around and around. This kind of periodic motion is called rotation. If the energy is just equal to the critical value, there will be two possibilities. 

 If the pendulum starts out in motion, it will approach its vertical position ever more closely, without reaching it in any finite time. Or, the pendulum could start out perched exactly in the vertical position. It will remain there indefinitely. If the energy is zero (k = 0,  w = 0), the pendulum just hangs straight down in a vertical plumbline.  

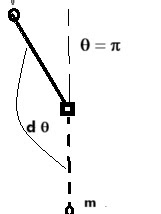
We now examine the case for k < 1 which means the angle q (or f)  can have any value, since  f =  q /2 .  The diagram below can be of help:

Here, we have the case for k = 1 which means that as f  ®  3p /2 the integral  ® oo  as t  ® oo.  As the pendulum approaches an upright position it takes "an infinite time" to do it.  Let's break the problem template down in summary:

1) The independent variable for this approach is the time, t.  The dependent variable is x or q .

2) If the solution x(t) is known, then x'(t) is found by differentiation.  This is an example of a problem with one degree of freedom.  All such problems in mechanics can be completely solved. 

3) A particular solution requires knowing the value of 2 constants of integration. 

Suggested Problem:

The motion of the  pendulum below is studied as part of a celestial mechanics course, where   c  is the critical torque for which  f =  p /2.

a) Write an appropriate equation for the critical torque value using the parameters: m (for pendulum mass), R for radius of motion, and g (acceleration of gravity).

b) If the value of  c   is exceeded then the applied torque becomes larger than the restoring torque. Write an inequality expressing this condition.

c) Write out one  plausible form for the integral: òÖA dt.

d) To have libration we need k > 1. Write an appropriate integral for this.

e) Given the condition sin f »   f   show the motion would be simple harmonic and write an equation for the characteristic frequency, w o.