Curves in 3-Space:
As previously defined, every point in the space R 3 is uniquely determined by a position vector x = (x1 , x2 , x3). Then in order to introduce the concept of a curve we use a real vector function: x = x(t) and this will have components:
x1 = x1 (t) x2 = x2 (t) x3 = x3 (t)
Which are single-valued functions of real variable t defined in the interval: I: a < t < b. To every value of t a point of R 3 is associated whose position vector is x(t).
Then the vector function determines a point set M in R 3 which we call a parametric representation of the set M, and the variable t is called the parameter of the representation. Given the above and that the trivial case of M = 1 point is discarded while the vector function must have multiple derivatives, we may assume:
1) The functions xi = xi (t) (i=1,2,3.....) are r (> 1) times continuously differentiable in I where the value of r will depend on the problem under consideration.
2) For every value of t in I, at least one of the three functions:
xi (t) = d xi (t)/ dt
is different from zero.
Definition: Arc of a curve:
If an arc is simple the correspondence between the points and the values of the parameter t is one to one. In this case not only is the functional relation of the points to the values of t continuous but also the inverse relation, i.e. the relation of the values of t to the points.
Definition: A curve:
A point set is called a curve if it can be represented by an equivalence class of the form x = x(t) whose interval I is not assumed to be closed or bounded, but is such that one always obtains the arc of a curve if the values of the parameter t are restricted to any closed and bounded subinterval of I.
A curve is said to be closed if it possesses at least one representation which is periodic, i.e.. of the form: x(t + w ) = x(t)
Thus the circle: x(t) = (r cos t, r sin t, 0) with r 2 = 4 is an example of a simple closed curve.
Thus, we have: x1 = r cos t , x 2 = r sin t, x 3 = 0
-> x 1 2 + x 2 2 = r 2 (cos 2 t + sin 2 t) = 4
So, the circle is closed and in the x 1 x 2 -plane, e.g.
Special curves: A few special curves and their representations are now examined. The main proviso here is to point out that there are curves of the form x = x(t) that cannot always be represented as a whole in the forms: x 2 = x 2 (x 1), x 3 = x 3 (x 1). This difficulty will occur when one value of the independent variable corresponds to several values of the dependent one, since the concept of a function requires a 1:1 onto correspondence of dependent to independent variable. Thus, in the case of the circle, a representation of the form just highlighted would be:
x 2 = + Ö ( r 2
- x
1 22) x 3 = 0
If we choose the + sign, we have a semicircle in the upper half plane. If we choose the negative sign we have a semicircle in the other half plane.
Ellipse with center at origin of coordinate system in space. In the parametric representation we can write (analogous to that for the circle): x(t) = (a cos t, b sin t, 0)
Or:
x 1 2 / a 2 + x 2 2 / b 2 = 1, x 3 = 0
If the principal axes have lengths 2a and 2b (say with a = 8, b = 16), respectively and coincide with the x 1 and x 2 axes, respectively, we obtain the graph shown below:
And note that if a= b = r we just recover a circle:
x(t) = (r cos t, r sin t, 0)
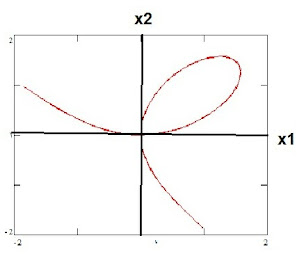
The folium of Descartes: This can be expressed in parametric form as:
x(t) = (3t/ 1 + t3 , 3t2/ 1 + t3 , 0)
This curve will be found to lie in the 1st, 2nd and 4th quadrant of the x 1 - x 2 plane as shown below:
By inspection the reader will also see it has a double point at (x 1 , x 2) = (0, 0) . Note also that part of the curve in the 2nd quadrant corresponds to values of t from -1 to 0, while the loop in the first quadrant corresponds to values between 0 and ¥. In the 4th quadrant the t-values range from - ¥ to -1.
The circular helix:
The parametric form here is: x(t) = (r cos t, r sin t, ct) c ≠ 0. The orthogonal projection of the helix into the x 1 x 2 - plane, e.g.
is the circle:
x 1 2 + x 2 2 - r 2 = 0, x 3 = 0
which is the intersection of this plane with the cylinder of revolution on which the helix lies. Projecting the helix orthogonally into the x2 x 3 - plane we obtain the sine curve:
x2 - r sin (x 3 /c) = 0, x 2 = 0
A cosine curve will be obtained by projecting the helix orthogonally into the x 1 x 2 - plane.
Suggested Problems:
1) Sketch the graphs of;
x 2 = - Ö ( 8 2 - x 1 22)
And:
x 2 = - Ö ( 16 2 - x 1 22)
On the same Cartesian axes
2)(a) Write the polar form of the equation of the line:
3 x 1 + 4 x 2 = 5
b)Determine the polar (r, q) equation for :
x 1 2 + x 2 2 - 2ax 2 = 0, a ≠ 0
And sketch the resulting curve
3)(a) Let r and q be polar coordinates in the x 1 x 2 - plane. Give the representation of the following curve in Cartesian coordinates:
r = a q
And sketch it.
b) A student's analysis of the curve (cardioid):
r = 6 (1 - cos q), is shown below:
Using differential calculus show how an expression for the angle y can be obtained in terms of the angle q.





No comments:
Post a Comment