We know that observable quantities - like a sunspot's magnetic field intensity - are all, by necessity, real numbers—but the underlying wavefunctions and quantum states usually involve the unphysical number i, or Ö -1. Also, the presence of i in QM is not just ancillary or peripheral to the phenomenon, such as the intensity distribution associated with an ideal diffraction grating, e.g.
A exp(i q) = a [ 1 + e id + e i2d + e i3d +....... exp(i(N-1) d)
It is rather central and intrinsic to the wave function y (r,t) peculiar to both the Schrodinger and Heisenberg formulations. But one is led to ask: Are imaginary numbers a necessary feature of the theory, or are they just an artifact of its formulation, so that an all-real formulation could be found that works just as well? This topic came up in a recent issue of Physics Today, in the article by Johanna L. Miller, who writes:
"That’s a subtle question. One can always represent the space of complex numbers as a two-dimensional space of real numbers, with one dimension representing a complex number’s real part and the other the imaginary part."
See, for example, my previous post on the topic:
But as Miller notes, "quantum states themselves are represented mathematically as multidimensional spaces—and as it turns out, the combination of dimensions upon dimensions significantly complicates the mathematics of how quantum systems interact."
The fastest, most expeditious way to grasp this is to compute the probability density for the quantum wave function. In general, one is interested in where a single particle (say hydrogen electron) is located in a given volume so that we can write:
y (r,t) y *(r,t) dV
For the probability the particle lies somewhere in an element of volume dV. More specifically and after applying the normalization condition, to locate the particle between a* and a:
P aa’ = ò a’a ‖y‖2 dx = 1
We note that for the electron in the 1s state we have: P = ½y (1s) y (1s) *½
Yielding the graphic result:
This is the giveaway for all subatomic behavior showing that the particle - in this case electron - cannot be localized to a position, say like a planet in celestial mechanics. We can only obtain a probability value for where it might be, not an exact, pinpointed location. This informs us that the QM wave function or state function is not the same as say the wave function for electromagnetic (EM) waves. For example, in the latter case, radio astronomers can precisely locate the position of an object emanating EM radio waves by tracing back the source position from its radio flux e.g.
But no similar analogy applies for locating a particle using the wave function of QM. In their new work, as noted in the PT article, Miguel Navascués of the Austrian Academy of Sciences in Vienna and colleagues refine the question: Is it possible to formulate a version of quantum theory that retains some of the key mathematical properties of standard quantum theory—in particular, that the composition of two systems is represented by their tensor product—but that uses only real numbers? They found that the answer is no.
Navascués and colleagues devised an experiment for which any such real-valued theory predicts different results than standard quantum theory. The experiment is only a little more involved than the one used to test Bell’s inequality, e.g.
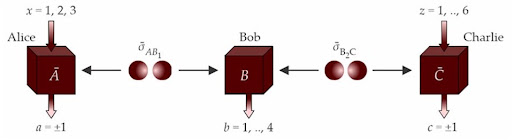
The basic set up of the Navascués et al experiment is shown in the diagram below:
Adapted from M.-O. Renou et al., Nature 600, 625 (2021)
Of two pairs of entangled particles, 'Bob' receives one of each, and the other two go to 'Alice' and 'Charlie'. Bob makes a joint measurement on his particles, and Alice and Charlie each choose from a few different measurements to make on theirs. As with Bell’s inequality, theories can be distinguished by the predictions they make about the correlations among the measurement outcomes.
Unlike with Bell’s inequality, however, calculating the expected correlations is extremely difficult. To find an upper bound for real-valued theories, Navascués and colleagues embarked on a computation so involved that they ran out of computer memory. They had to make do with a looser bound than they were hoping for. What they found was a computed value of 6Ö2 = 8.489 for standard quantum theory. However, the uppermost bound was 7.66, i.e. for a real-valued formulation.
There followed an experiment (by Jian -Wei Pan and colleagues at the University of Science and Technology of China) carried out using superconducting qubits, for which a value of 8.09 was observed. This comfortably put the result of the experiment in the realm of complex quantum theory. There followed yet another experiment (using photons) by a Chinese group based at Southern University of Science and Technology at Shenzhen which also vindicated complex QM.
Basically, from last January, two groups carried out the experiment—and both found results in favor of standard complex-valued quantum theory. But hold strain. According to the author of the PT piece (Johanna Miller) neither Chinese group "has closed the loopholes in their respective experiments." That means the jury is still out on whether real or complex numbers afford the better description of the quantum world. Never fear, however, I am confident those loopholes will soon be closed and complex -valued numbers will prevail. Call it a gut feeling.
Not yet mentioned, but pointed out by physicist David Bohm (Wholeness and the Implicate Order, pp. 237-38) , is the core role of complex numbers in the algebras that underpin quantum theory, i.e.
"It is significant
that by mathematizing the general language in terms of an initially undefined
and unspecified algebra, we arrive
naturally at the sort of algebras used in current quantum theory for ‘particles
with spin’, i.e. products of matrices and quaternions. These
algebras have in addition, however, a significance
going beyond that of technical calculations carried out in the quantum theory.
For example, the quaternions imply invariance
Related to this are the Pauli spin matrices, i.e.
Which occur in the Pauli equation taking into account the interaction between the of a particle spin and the external EM field. This and the fact that the pure states of a quantum mechanical system are represented by unit vectors in a complex separable Hilbert space, known as the state space, are convincing enough for me. That is, that the edifice of quantum mechanics is fundamentally based on complex -imaginary numbers.
Future students of quantum mechanics, it seems, will have no choice but to grapple with the mathematics of imaginary numbers. (M.-O. Renou et al., Nature 600, 625, 2021.) Which is not a bad thing given they already appear in so much of physics, i.e. the portrayal of the complex amplitudes associated with an ideal diffraction grating. Not to mention one particular form for unstable (electrostatic) plasma waves, e.g.
ikE = 4p e (ien o kE) [1/ m i - 1/ m(w - k vo )
Thus, the widespread use of complex numbers in physics, and their special meaning in QM prefigures their acceptance as the dominant formalism. Nonetheless the ongoing entanglement experiments -- apart from giving quantum physicists something to do - should point the way toward dealing with those onerous loopholes. (In whatever form they take)
See Also:



No comments:
Post a Comment