The Basic Laws Of Physics In A Nutshell (Part 1)

 The laws of physics may best be described as “the basic laws of the universe” since the total of accumulated evidence (e.g. gravimetric, spectrographic etc) discloses they apply everywhere in the cosmos. Alas, it is not a short list – but grouped according to different aspects: mechanical, thermal, electric-magnetic, etc.

Students have often asked me in the course of lectures: What laws constitute an essential list, say for a text book of physics or science? I reply consistently that the book must reflect or embody the basic laws we know of, else it can’t be described as any book of physics, or science. Are these laws rigorous? Yes, they are – and at the end we will also see by way of examples how and why certain reported “claims” can’t be justified because they violate one or other of these laws.

Let’s begin with the basic laws of mechanics – embodied in Newton’s laws of motion:

1) Any body at rest or in uniform motion remains at rest or in uniform motion unless acted on by an outside force.

2) The acceleration of an object is directly proportional to the resulting force acting on it (F = ma)

3) If 2 bodies interact, the force that body 1 exerts on body 2 is equal and opposite to the force that body 2 exerts on body 1.  (F(12) = F(21) = - F(12))

Newton’s law of universal gravitation:

Every particle in the universe attracts every other particle with a force directly proportional to the product of the masses, and inversely proportional the square of the distance between them. It may be written:

F = G Mm/ r²

where G is the universal Gravitational constant, M, m the two interacting masses, and r the distance between them.

Note: the behavior of freely falling objects, or what is colloquially called the “law of gravity” is actually a special case of the universal law applied to Earth and employing Newton’s 2nd law, such that:

F = ma = mg = GMm/ R_E²

where M is the mass of the Earth, m an object on it and R_E the radius of the Earth.

By algebra (m cancels on both sides):

g = GM/ R_E²

And if the body is at some height h above the surface (h added to the radius to get R) we know:

R = h + R_E

so

F = GM m/ R²    =  GM m/ (h + R_E)²   

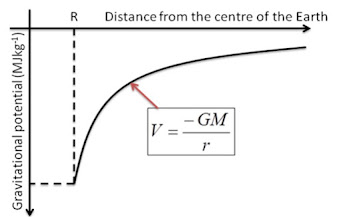
Gravitational potential:

One of the critical concepts to do with gravitation is that of gravitational potential, V .  We thereby imagine a mass m moved from a distance of infinity (¥) to the distance (radius) R from M. We inquire into the work done by the field over some dx. Then:

dW = F dx (dx is positive)

Then the attractive force is:

F = G Mm/ x²  so   V = ò _¥ ^R (GMm) dx/ x²

And: 

V = G M m  ò _¥ ^R  dx/ x² = GMm [-1/x] _¥ ^R

A graphical representation is given below for the case of V near Earth:

Law of Conservation of Linear Momentum:

In the law of conservation of linear momentum- let two masses m1 and m2 collide with each other with respective velocities v1 and v2, then the total linear momentum before collision must equal the total linear momentum after. Thus:

BEFFORE: m1v1(i) + m2 v2(i)

AFTER: m1v1(f) + m2 v2(f)

Where (i, f) subscripts denote initial and final values, so: P12(i) = P(12)f

Note the above law applies whether a collision is elastic or inelastic. The difference is that in the latter case, the mechanical energy (i.e. kinetic) is not conserved because some will be lost as heat due to friction.


Conservation of Angular Momentum:

This law applies to rotational motion. It states that the total angular momentum of a system is constant if the resultant external torque acting on the system is zero:

Thus IF: S d(T)_ext/ dt = dL/dt = 0

Then: I_i(w_i) = I_f (w_f )= const.

Where I_i, If are the initial and final moments of inertia, and w_i,_f denote the angular velocities.

The law (expression) is valid for rotations about a fixed axis or about an axis through the center of mass of the system.

To be continued in Part (2)