More Plasma Physics: Looking At Solitons And Soliton Solutions (Of The Korteweg deVries Equation)

 

In space plasma physics many situations arise in which one will wish to examine the behavior of a solitary wave - say in a particular plasma environment. One such is for nonlinear ion-acoustic waves. 

 The solitary wave (soliton) is just a traveling wave of form:  

u(x, t) =  f(x - ct)  

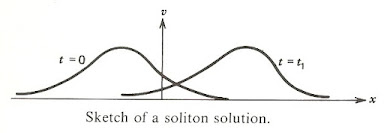
for some smooth function f that decays rapidly at infinity and under certain conditions can travel without change of shape (see graphic). 

  Consider the partial differential equation:

 u_tt   - u_xx  =   u ( 2 u²  -  1)

Which has a family of solitary wave solutions:

u(x,t) = sech (x cos q +   t sinh q)

We do not expect, for mathematical reasons,  the sum of two such solutions (superposition) to also be a solution.  There is, however, a class of soliton equations which does exhibit a form of nonlinear superposition.  An n-soliton solution then is a solution that is asymptotic to a nontrivial sum of n solitary waves, e.g.

å ⁿ_t=1 f _i  (x - c_i  t) as t -> - oo  and to the sum of the same waves:

å ⁿ_t=1 f _i  (x - c_i  t  + r_i)

with non-zero phase shifts r_i  as t -> oo.  I.e. after nonlinear interaction the individual solitary waves pass through each other, keeping their velocities and shapes - but with phase shifts. 

 The  Korteweg de Vries (KdV) equation:

(- v _o  + c _s   + v) ¶  v / ¶x’  -  m ¶ ² v / ¶x²’  

+  a ¶ ³ v / ¶x³ =  0

is a well known example of  such a soliton equation admitting nonlinear superposition.  Here c _s is the ion sound speed, and v _o the  electron thermal speed.  In the form shown we note the appearance of the dissipative term (m ¶ ² v / ¶x²)  and that for a soliton to evolve into a shock a dissipative mechanism is needed.  In the more common situation steepening of the wave balances dispersion and one will obtain a wave  form such a shown in the top graphic. We focus more on this case now by adjusting the KdV equation.

  On integrating once,  and excluding the shock evolution term (in m) ,  we obtain:

a  d² V/ dx²   -    (v _o   -   c _s ) v  -   v ²/ 2   =  0 

Which has the same mathematical form as Newton's 2nd law of motion, e.g.  m x" =  F(x)  =   -  ¶ x V(x)  

Where V(x) is the potential energy. With some further manipulation we find:

a d² V/ dx²   =   -  ¶ v  V' (x)  =

-  ¶ v [(c _s   -  v _o) v ²/ 2   +     v³/ 6 ]

For a particle 0f mass a   moving under a potential field given by the quantity in brackets.  We call this quantity the pseudo potential and designate it:

 F (v) =  [(c _s   -  v _o) v ²/ 2   +     v³/ 6 ]

Which is also known as the Sagdeev potential.  It is left to the industrious reader to do a simple plot of  F (v) vs.  v,   with   v _max   shown on v -axis.

For the criteria on  F  to obtain a soliton solution we have:

i)   ¶ F / ¶ V ] _{v= 0}  =  0;  ¶ ² F/ ¶ v²   <   0

ii)  F   <   0,   For   0   <   v   <   v _max

iii)  d F / d V ] _{v= v max}  >  0

We  note here that two graphs of  F   vs.  v are possible,  one for  c _s   -  v _o   >   0,  the other for  c _s   -  v _o   <   0.  Since we demand only a localized wave form then it will always be the latter form used, i.e. in further analyses.  One such is to obtain a soliton solution for the KdV equation:

a  d² V/ dx²   -    (v _o   -   c _s ) v  -   v ²/ 2   =  0 

This may be solved exactly i.e. with c _s   -  v _o   <   0.   The procedure is then to multiply the KdV by v'  and then integrate to obtain:

a/ 2  (v' ²)  =  (v _o   -   c _s ) v ²/ 2  -    v³/ 6

And we choose the constant of integration to be zero because we want v' = 0  when  v = 0.   Working through the process the final solution is found to be:

v   =   3 (v _o   -   c _s ) sech ²  [(v _o   -   c _s  / 4 a) ½     x' ]

Suggested Problems:

1)  Plot a graph of  F   vs.  v  for the case c _s   -  v _o   <   0 and indicate the position of v _max  on the graph.

2)  Integrate  the KdV equation:

a  d² V/ dx²   -    (v _o   -   c _s ) v  -   v ²/ 2   =  0 

And show how the soliton solution:

v   =   3 (v _o   -   c _s ) sech ²  [(v _o   -   c _s  / 4 a) ½     x' ]

Is obtained.  Given this is in the fluid frame, show what it would be in the lab frame.