One of the key tasks for planetary astronomers - amateur or professional - is to ascertain the point at which a superior planet's motion changes from being retrograde to direct. I are referring here to the planet's geocentric (Earth-centered or referenced) angular velocity, and identifying when it becomes direct - between opposition and quadrature (see previous blog instalments for these configuration definitions).
Clearly, if such a change occurs, there will be some point the motion is neither retrograde or direct and this is called a "null" point or better, "stationary point". The problem then, is to obtain an expression for the planet's elongation E at a stationary point in terms of the distances of the planet and Earth from the Sun. Using such an expression and the measured elongation, the planet's heliocentric distance can be computed. (In addition, we can also obtain an analytical expression giving the angle Θ between the heliocentric radius vectors of planet and Earth at the stationary point) Further, such an analytic expression together with the synodic period of the planet, allows us to predict its next stationary point.
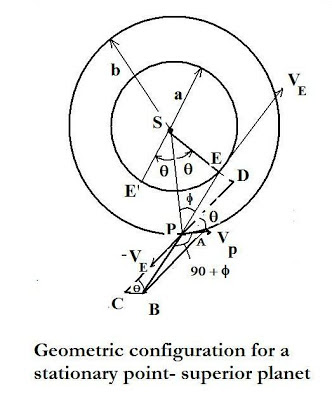
To fix ideas here, we use the accompanying diagram and let the positions of Earth and planet at the stationary point be denoted by E and P. The velocity of P relative to E must lie along the geocentric radius vector (EP) if the planet appears stationary. As we learned in the "Basic Physics" blogs, we can form a "parallelogram" of velocities - just as we can for forces. In this case, we can form the velocity parallelogram PABC, with the resultant given by PB.(E.g. the resultant of the vectors (- V E) and the planet's tangential velocity Vp. Note that: PA = Vp and PC = -V E
Clearly, if such a change occurs, there will be some point the motion is neither retrograde or direct and this is called a "null" point or better, "stationary point". The problem then, is to obtain an expression for the planet's elongation E at a stationary point in terms of the distances of the planet and Earth from the Sun. Using such an expression and the measured elongation, the planet's heliocentric distance can be computed. (In addition, we can also obtain an analytical expression giving the angle Θ between the heliocentric radius vectors of planet and Earth at the stationary point) Further, such an analytic expression together with the synodic period of the planet, allows us to predict its next stationary point.
To fix ideas here, we use the accompanying diagram and let the positions of Earth and planet at the stationary point be denoted by E and P. The velocity of P relative to E must lie along the geocentric radius vector (EP) if the planet appears stationary. As we learned in the "Basic Physics" blogs, we can form a "parallelogram" of velocities - just as we can for forces. In this case, we can form the velocity parallelogram PABC, with the resultant given by PB.(E.g. the resultant of the vectors (- V E) and the planet's tangential velocity Vp. Note that: PA = Vp and PC = -V E
Since we assume the orbits are circular (a close enough approximation) the angle Θ between the heliocentric radius vectors must be angle PCB between the velocity vectors. In addition, note that angle APB = 90 + φ. Now, if we extend CP to meet the line SE (produced at D) then angle DPA = Θ and angle EPD = 90 - (Θ + φ). Focusing now on the triangle PCB, we may use the sine formula of trigonometry to write:
sin[90 - (Θ + φ)] / Vp = sin (90 + φ) / V E
or (using trigonometric identities):
cos (Θ + φ) = (Vp / V E) cos φ
Making use of another trig identity and triangle SEP, we may write:
SP = PE cos φ + SE cos Θ
or:
(I) b = PE cos φ + a cos Θ
Applying it once more to triangle SEP we get:
SE = SP cos Θ + PE cos (SEP)
or:
(II) a = b cos Θ + PE cos (Θ + φ)
From the geometry of the configuration, since angle SEP = 180 - (Θ + φ), we can write equations (I) and (II) as:
(Ia) b - a cos Θ = PE cos φ
and:
(IIa) a - b cos Θ = PE cos (Θ + φ)
Dividing through eqn. (Ia) by eqn. (IIa):
[b - a cos Θ]/ [a - b cos Θ] = cos φ/ [cos (Θ + φ)]
Now, cos (Θ + φ) = (Vp / V E) cos φ
And we know:
(V2/V1) = Ö (a1/a2 )
Combining these in (Ia) and (IIa) we have:
[b - a cos Θ]/ [a - b cos Θ] = (Vp / V E) = Ö (b /a)
Algebraically re-arranging we find:
cos Θ = [Ö a Ö b (Ö a + Öb)] / (a 3/2 + b3/2 )
The preceding can be vastly simplified if all units are normalized to those in terms of Earth's to the Sun. Thus, a = 1 and b is in terms of a. So let:
Ö Q = Ö a Ö b
(1 + Ö Q) = (a 3/2 + b3/2 )
Then re-write as:
cos Θ = [Ö Q (1 + Ö Q) ]/ (1 + Q 3/2)
As may be discerned from the diagram, when Earth is at point E' where angle ESP = 90 degrees, we have another stationary point. It is of interest here to compute the total time during which a planet will be seen to move retrograde and this is just the time it takes Earth's radius vector to advance through an angle equal to 2 Θ, with respect to the planet's radius vector. This will be given by t( Θ), where:
t( Θ) = 2 Θ/ 360 x S X (ΘS)/ 180
where S is the synodic period.
The time that elapses between opposition and the next stationary point is just t( Θ)/2.
Meanwhile, the time interval during a synodic period that a planet's motion is direct is t(D) where:
t(D) = (360 - 2 Θ)/ 360 X S X (1 - Θ/ 180)S
Example Problem:
Mars has a synodic period S = 779.9 days. At a particular stationary point Mars' radius vector is determined to be 1.52 AU. Find the angle Θ that Earth would have advanced to reach this point and time elapsed between opposition and the next stationary point .
Solution:
We have:
cos Θ = [Ö Q (1 + Ö Q) ]/ (1 + Q 3/2)
where:
Ö Q = Ö a Ö b = Ö (1) (1.52) = 1.23
(1 + Q 3/2) = Ö a + b 3/2 = 1 + (1.52) 3/2 = 1 + 1.87 = 2.87
Then:
cos Θ = [ Ö (1.23) (2.23) ] / (2.87)
cos Θ = [(1.10)(2.23)]/ (2.87) = 1.64/2.87 = 0.571
Θ = arc cos [0.571] = 55.1 deg
The time that elapses between opposition and the next stationary point is just:
t( Θ)/2= ½ [2 Θ/ 360 x S X (ΘS)/ 180 ]
Where: S = 779.9d/ 365.25 d = 2.13 yrs
So:
t( Θ)/2= ½ [(110.2)/ 360 x (2.13) X (55.1 x 2.13)/ 180 ]
t( Θ)/2= ½ [(0.306) (2.13) (0.652)] = 0.21 yrs.
Problems for Budding Astronomers:
1) Mars reaches a stationary point 36 ½ days after opposition. Its elongation is then measured to be 136.2 deg. Given that the sidereal period is 687 days, find the distance of Mars from Earth in AU. Also, find the time to its next stationary point.
2) Find the length of time Jupiter has retrograde motion in each synodic period given its heliocentric distance is 5.2 AU and its sidereal period is 11.86 years.
3) In the Epsilon Eridani star system a planet designated Epsilon Eridani III is determined to have the exact same orbital parameters as Earth (e.g. a, e, i etc.).
In the same system, another exoplanet designated Epsilon Eridani IV is found to have Vp = 4.5 km/s.
1) Mars reaches a stationary point 36 ½ days after opposition. Its elongation is then measured to be 136.2 deg. Given that the sidereal period is 687 days, find the distance of Mars from Earth in AU. Also, find the time to its next stationary point.
2) Find the length of time Jupiter has retrograde motion in each synodic period given its heliocentric distance is 5.2 AU and its sidereal period is 11.86 years.
3) In the Epsilon Eridani star system a planet designated Epsilon Eridani III is determined to have the exact same orbital parameters as Earth (e.g. a, e, i etc.).
In the same system, another exoplanet designated Epsilon Eridani IV is found to have Vp = 4.5 km/s.
a) Using your knowledge of the known parameters, plus the diagram shown, construct an appropriate parallelogram of velocities and hence obtain the angles: Θ and φ.
b) Hence, or otherwise, estimate the time planet Epsilon Eridani IV will be moving retrograde relative to Epsilon Eridani III, and also the time between its opposition and the next stationary point.
c) Obtain the time during Epsilon Eridani IV's synodic period that it is moving direct.
No comments:
Post a Comment